Question

已知Rt△AOB，其中∠AOB=90°，OA=6，OB=8．将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边OB交于点C，与边AB交于点D．
（1）如图（1），若折叠后使点B与点O重合，则点D的坐标为______；
（2）如图（2），若折叠后使点B与点A重合，求点C的坐标；
（3）如图（3），若折叠后点B落在边OA上的点为B′，是否存在点B′，使得四边形BCB′D是菱形？若存在，请说明理由并求出菱形的边长；若不存在，请说明理由．

Answer 1

解：（1）∵OA=6，OB=8
∴A的坐标是（6，0），B的坐标是（0，8），
D是AB的中点，则坐标是：（3，4）；
（2）设C（0，m），（m＞0），
则CO=m，
BC=AC=（8-m），
在Rt△AOC中，有（8-m）²-m²=36，
整理得，16m=28，
∴，
∴C（0，）；
（3）存在，当B'C∥AB（或B'D∥BO）时，四边形BCB'D是菱形，
∵∠AOB=90°，OA=6，OB=8，∴AB=10，
∵B'C∥AB，∴△OB'C∽△OAB，∴，
设B'C=BC=x，则，
解得，，
∵B'C∥AB，
∴∠CBD+∠BCB'=180°，
又∵∠CBD=∠CB'D，∴∠CB'D+∠BCB'=180°，
∴B'D∥BO，
∴△AB'D∽△AOB，
∴，
设B'D=BD=y，
∴，
解得：，
∴B'C=BC=B'D=BD，
∴四边形BCB'D是菱形，
∴存在点B'，使得四边形BCB'D是菱形，此时菱形的边长为．
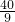
分析：（1）A是直线AB的中点，则D的坐标即可求解；
（2）折叠后使点B与点A重合，则C在AB的中垂线上，Rt△AOC中利用勾股定理即可得到方程，求得C的坐标；
（3）当B'C∥AB（或B'D∥BO）时，四边形BCB'D是菱形，则△OB'C∽△OAB，依据相似三角形的对应边的比相等即可求得B′C的长度，然后根据△AB'D∽△AOB，即可求得B′D的长．从而证得B'C=BC=B'D=BD．
点评：本题是勾股定理、相似三角形的判定与性质、菱形的性质的综合应用．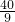