Question

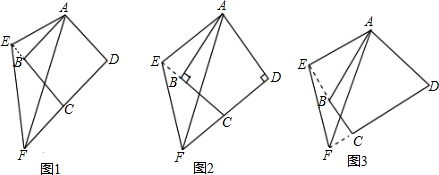
(1)如图(1)，在△ABC中，∠C＞∠B，AD⊥BC于D，AE平分∠BAC，则∠EAD与∠B、∠C有何数量关系？

(2)如图(2)，AE平分∠BAC，F为其上一点，且FD⊥BC于D，这时∠EFD与∠B、∠C又有何数量关系？

(3)如图(3)，AE平分∠BAC，F为AE延长线上一点，FD⊥BC于D，这时∠AFD与∠B、∠C又有何数量关系？

Answer 1

答案：
解析：

答案：(1)∵AE平分∠BAC∴∠BAE＝∠BAC∵∠BAC＝180°－∠B－∠C∴∠BAE＝(180°－∠B－∠C)＝90°－∠B－∠C∵∠AED＝∠B＋∠BAE

提示：

在处理三角形中的角的问题时，有时需要从整体出发进行考虑，有时也可以通过适当添加辅助线使未知问题转化为已经解决的问题．本题中第(1)问要找出∠EAD与∠B、∠C的数量关系，可考虑利用三角形内角和等于180°及三角形的外角性质．为此，把∠EAD、∠B、∠C先放到具体的三角形中，∠EAD可看做△ADE的一个内角，也可看做∠EAC与∠DAC的差或∠BAD与∠BAE的差． 　　本题第(2)、(3)小题，可先作出BC边上的高，得到∠EAG，再确定∠EFD(如图(2)、图(3))．