练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    分别画一个四边形，五边形，六边形，数一数它们的对角线的条数，并说明多边形对角线的条数与它的边数有何关系？

    答案：
    解析：

    　　解：①四边形两条对角线，五边形五条，六边形九条．

    　　②对角线条数与边数有下面的关系：

    　　2＝，5＝，9＝；

    　　③通过观察发现，从n边形的一个顶点出发可以引(n－3)条对角线，n个顶点可引n(n－3)条，而其中的每一条都计算了两次，所以由归纳可以猜想：

    　　n边形的对角线条数为．

    　　说明：本题主要考查思维能力的开放性，从特殊到一般探讨多边形对角线的条数．


    提示：

    提示：用从特殊到一般的思想，用归纳比较的方法，归纳总结出多边形的对角线与边数间的关系．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    26、探究题
    如下图所示，已知平面内A、B、C、D、E五个点．
    （1）按要求画出图形：
    ①画直线AC；
    ②画射线EA、EC；
    ③连接AB、BC、CD、DA．
    （2）在（1）所画的图形中，任意找出一个锐角和一个钝角，并将它们分别表示出来：
    锐角：
    ∠EAC

    钝角：
    ∠AEC

    （3）①用量角器量出四边形AECD的四个内角的度数，即∠DAE、∠AEC、∠ECD、∠CDA的度数分别为
    50°，150°，60°，90°
    ，这四个内角的度数和为
    360°
    ；
    ②用量角器量出四边形ABCD的四个内角的度数，即∠DAB、∠ABC、∠BCD、∠CDA的度数分别为
    90°，70°，110°，90°
    ，这四个内角的度数和为
    360°
    ．从以上的操作中，你有什么发现？（只需写出结论）

    查看答案和解析>>

    科目：初中数学 来源：新教材完全解读　九年级数学　(下册)　(配华东师大版新课标) 华东师大版新课标 题型：044

    阅读并解答下列问题．

    在给定的锐角△ABC中，求作一个正方形DEFG，使D，E落在BC边上，F，G分别落在AC，AB边上，作法如下．

    第一步：画一个有三个顶点落在△ABC两边上的正方形；

    第二步：连结并延长交AC于点F；

    第三步：过F点作FE⊥BC，垂足为点E；

    第四步：过F点作FG∥BC交AB于点G；

    第五步：过G点作GD⊥BC，垂足为点D．

    四边形DEFG为所求作的正方形．如图所示．

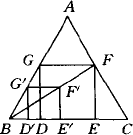
    (1)证明上述所求作的四边形是正方形(EF＝FG)

    (2)在△ABC中，如果BC＝6＋，∠ABC＝45°，∠BAC＝75°，求上述正方形DEFG的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    探究题
    如下图所示，已知平面内A、B、C、D、E五个点．
    （1）按要求画出图形：
    ①画直线AC；
    ②画射线EA、EC；
    ③连接AB、BC、CD、DA．
    （2）在（1）所画的图形中，任意找出一个锐角和一个钝角，并将它们分别表示出来：
    锐角：______
    钝角：______
    （3）①用量角器量出四边形AECD的四个内角的度数，即∠DAE、∠AEC、∠ECD、∠CDA的度数分别为______，这四个内角的度数和为______；
    ②用量角器量出四边形ABCD的四个内角的度数，即∠DAB、∠ABC、∠BCD、∠CDA的度数分别为______，这四个内角的度数和为______．从以上的操作中，你有什么发现？（只需写出结论）

    查看答案和解析>>

    科目：初中数学 来源：山东省期末题 题型：解答题

    如下图所示，已知平面内A、B、C、D、E五个点。
    （1）按要求画出图形：
    ①画直线AC；
    ②画射线EA、EC；
    ③连接AB、BC、CD、DA；
    （2）在（1）所画的图形中，任意找出一个锐角和一个钝角，并将它们分别表示出来：
    锐角：______，
    钝角：______；
    （3）①用量角器量出四边形AECD的四个内角的度数，即∠DAE、∠AEC、∠ECD、∠CDA的度数分别为______，这四个内角的度数和为______；
    ②用量角器量出四边形ABCD的四个内角的度数，即∠DAB、∠ABC、∠BCD、∠CDA的度数分别为______，这四个内角的度数和为_______从以上的操作中，你有什么发现？只需写出结论）

    查看答案和解析>>

    同步练习册答案