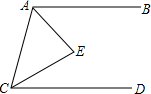
解:(1)①∠APC=∠PAB+∠PCD,
过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∴∠APC=∠1+∠2=∠PAB+∠PCD;
②∠PAB+∠APC+∠PCD=360°.
过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1+∠PAB=180°,∠2+∠PCD=180°,
∴∠PAB+∠APC+∠PCD=360°;
③∠PAB=∠APC+∠PCD.
延长BA,交PC于点E,
∵AB∥CD,
∴∠1=∠PCD,
∴∠PAB=∠APC+∠1=∠APC+∠PAD;
④∠PCD=∠PAB+∠APC,
∵AB∥CD,
∴∠1=∠PCD,
∴∠PCD=∠1=∠APC+∠PCD;
故答案为:①∠APC=∠PAB+∠PCD,②∠PAB+∠APC+∠PCD=360°,③∠PAB=∠APC+∠PCD,④∠PCD=∠PAB+∠APC;
(2)选择①.
证明:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∴∠APC=∠1+∠2=∠PAB+∠PCD.
分析:(1)①过点P作PE∥AB,利用平行线的性质,易得∠APC=∠1+∠2=∠PAB+∠PCD;
②过点P作PE∥AB,利用平行线的性质,易得∠PAB=∠APC+∠1=∠APC+∠PAD;
③延长BA交PC于点E,利用平行线与三角形外角的性质,可求得答案;
④利用平行线与三角形外角的性质,可求得答案.
(2)根据(1)中的结论,求解即可.
点评:此题考查了平行线的性质以及三角形外角的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.


 解:(1)①∠APC=∠PAB+∠PCD,
解:(1)①∠APC=∠PAB+∠PCD,

 阅读快车系列答案
阅读快车系列答案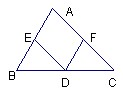 39、填写推理理由
39、填写推理理由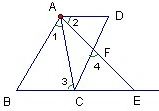 解:∵AB∥CD(已知)
解:∵AB∥CD(已知)