
如图,△
ABC是边长为2的等边三角形,E是AB边的中点,延长BC到点D,使CD=BC,连接ED.求ED的长.
|
分析:题设中既没有明显的,也没有隐含的垂直、直角等能构成直角三角形的条件.事实上,连接 AD,由△ABC为等边三角形,可得∠BAC=∠ACB=60°;再由△ACD为等腰三角形,可得△ABD和△AED均为直角三角形.解:连接 AD.因为△ ABC是等边三角形,所以∠ BAC=∠ACB=60°,∠ACD=120°.又因为 AC=CD,所以△ACD是等腰三角形.所以∠ CAD=∠CDA=从而∠ BAD=∠BAC+∠CAD=90°.则△ ABD和△AED均为直角三角形.在 Rt△ABD中,AD2=BD2-AB2=42-22=12,所以在Rt△AED中,ED2=AE2+AD2=12+12=13.所以 ED=点评:这种构造直角三角形的方法在解决有关几何问题时非常有效. |


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
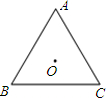 如图,△ABC是边长为a的等边三角形,O为△ABC的中心.将△ABC绕着中心O旋转120°.
如图,△ABC是边长为a的等边三角形,O为△ABC的中心.将△ABC绕着中心O旋转120°.查看答案和解析>>
科目:初中数学 来源: 题型:
 点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•溧水县一模)如图,△ABC是边长为4的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连结BD,交AC于F.
(2013•溧水县一模)如图,△ABC是边长为4的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连结BD,交AC于F.查看答案和解析>>
科目:初中数学 来源: 题型:
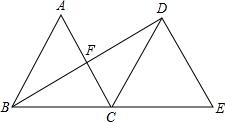 (2012•湘潭)如图,△ABC是边长为3的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连接BD,交AC于F.
(2012•湘潭)如图,△ABC是边长为3的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连接BD,交AC于F.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点做一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为
如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点做一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com