练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，河的两岸互相平行，紧靠河的北岸有一排间距为9米电线杆，紧靠河的南岸有一排间距为3米的柳树，某人在河的南岸面向河流观察发现，观看电线杆C恰被树A挡住，观看电线杆D恰被树B挡住，CD间有3个电线杆，AB间有2棵树，若此人距离河的南岸OE＝8米，求此河的宽度．

    答案：24米
    解析：

    延长OE交CD于F

    ∵AB//CD∴∠ABO＝∠CDO．

    又∠COD是公共角，

    ∴△AOB∽△COD，

    ∴ ．

    据题意知AB＝9米，CD＝36米，OE＝8米，设EF＝x，

    则：．

    解得：．

    答：河宽24米．


    提示：

    观察图形，根据题意可以得到△AOB∽△COD，再根据相似三角形对应边上的高之比等于相似比可以使问题得到解决．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

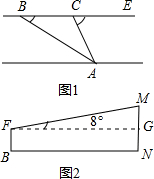    在一次课外实践活动中，同学们要测湘江河的宽度．如图1所示，小明先在河西选定建筑物A，并在河东岸的B处观察，此时视线BA在河岸BE所成的夹角∠ABE=32°，小明沿河岸BE走了400精英家教网米到C处，再观察A，此时视线CA与河岸所成的夹角∠ACE=64°．
    （1）请你根据以上数据，帮助小明计算出湘江河的宽度（结果精确到0.1米）．
    （2）求出湘江河宽后，小明突发奇想，欲求B的正对岸建筑物的高度MN（如图2所示），现测得小明的眼睛与地面的距离（FB）是1.6m，看建筑物顶部M的仰角（∠MFG）是8°，BN为湘江河宽，求建筑物的高度MN（结果精确到0.1米）．
    （提示：河的两岸互相平行；参考数值：sin32°≈0.530；cos32°≈0.848；
    tan32°≈0.625；sin64°≈0.900；cos64°≈0.438；tan64°≈2.050；
    sin8°≈0.139；cos8°≈0.990；tan8°≈0.141）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，要在一条河上架一座桥MN（河的两岸互相平行，桥与河岸垂直），在如下四种方案中，使得E、F两地的路程最短的是（　　）
    A、精英家教网B、精英家教网C、精英家教网D、精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    在一次课外实践活动中，同学们要测湘江河的宽度．如图1所示，小明先在河西选定建筑物A，并在河东岸的B处观察，此时视线BA在河岸BE所成的夹角∠ABE=32°，小明沿河岸BE走了400米到C处，再观察A，此时视线CA与河岸所成的夹角∠ACE=64°．
    （1）请你根据以上数据，帮助小明计算出湘江河的宽度（结果精确到0.1米）．
    （2）求出湘江河宽后，小明突发奇想，欲求B的正对岸建筑物的高度MN（如图2所示），现测得小明的眼睛与地面的距离（FB）是1.6m，看建筑物顶部M的仰角（∠MFG）是8°，BN为湘江河宽，求建筑物的高度MN（结果精确到0.1米）．
    （提示：河的两岸互相平行；参考数值：sin32°≈0.530；cos32°≈0.848；
    tan32°≈0.625；sin64°≈0.900；cos64°≈0.438；tan64°≈2.050；
    sin8°≈0.139；cos8°≈0.990；tan8°≈0.141）

    查看答案和解析>>

    科目：初中数学 来源：2011年3月浙江省杭州市下城区九年级（下）阶段性检测数学试卷（解析版） 题型：解答题

    在一次课外实践活动中，同学们要测湘江河的宽度．如图1所示，小明先在河西选定建筑物A，并在河东岸的B处观察，此时视线BA在河岸BE所成的夹角∠ABE=32°，小明沿河岸BE走了400米到C处，再观察A，此时视线CA与河岸所成的夹角∠ACE=64°．
    （1）请你根据以上数据，帮助小明计算出湘江河的宽度（结果精确到0.1米）．
    （2）求出湘江河宽后，小明突发奇想，欲求B的正对岸建筑物的高度MN（如图2所示），现测得小明的眼睛与地面的距离（FB）是1.6m，看建筑物顶部M的仰角（∠MFG）是8°，BN为湘江河宽，求建筑物的高度MN（结果精确到0.1米）．
    （提示：河的两岸互相平行；参考数值：sin32°≈0.530；cos32°≈0.848；
    tan32°≈0.625；sin64°≈0.900；cos64°≈0.438；tan64°≈2.050；
    sin8°≈0.139；cos8°≈0.990；tan8°≈0.141）

    查看答案和解析>>

    同步练习册答案