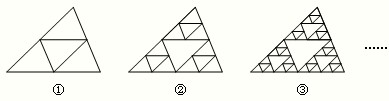
n
2-n+1
分析:根据前5个图形圆点的个数的变化不难发现后一个图形比前一个图形多的点数正好是连续偶数,然后利用求和公式求出第n个图形的圆点的个数的表达式即可得解.
解答:第1个图形有1个点,S
1=1,
第2个图形有3个点,S
2-S
1=3-1=2×1,
第3个图形有7个点,S
3-S
2=7-3=4=2×2,
第4个图形有13个点,S
4-S
3=13-7=6=2×3,
第5个图形有21个点,S
5-S
4=21-13=8=2×4,
…,
依此类推,第n个图形的点数为S
n,则S
n-S
n-1=2(n-1),
所以,S
1+S
2-S
1+S
3-S
2+S
4-S
3+S
5-S
4+…+S
n-S
n-1=1+2×1+2×2+2×3+2×4+…+2(n-1),
所以,S
n=1+2[1+2+3+4+…+(n-1)]=1+2×
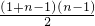
=n
2-n+1,
即第n个图形圆点的个数为:n
2-n+1.
故答案为:n
2-n+1.
点评:本题是对图形变化规律的考查,根据前几个图形的菱形的数目,发现后一个图形比前一个图形多的圆点的个数是连续偶数是解题的关键,难点是求和公式的利用.


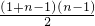 =n2-n+1,
=n2-n+1,