练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

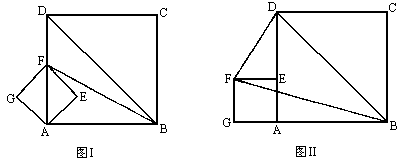
    如图Ⅰ，四边形AEFG与ABCD都是正方形，它们的边长分别为a、b(b≥2a)，且点F在AD上．(以下问题的结果可用a、b的代数式表示)

    (1)求S△DBF；

    (2)把正方形AEFG绕点A按逆时针方向旋转得图Ⅱ，求图中S△DBF；

    (3)把正方形AEFG绕点A旋转任意角度，在旋转过程中，S△DBF是否存在最大值、最小值？如果存在，试求出最大值、最小值；若不存在，请说明理由．

    答案：
    解析：

    略。


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

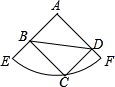    精英家教网如图，平行四边形ABCD中，E是AB上一点，DE与AC交于点F，且S△AEF=6cm2，S△DCF=54cm2，则S平行四边形ABCD=
     
    cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，在扇形AEF中，∠A=90°，点C为
    EF
    上任意一点（不与点E、F重合），四边形ABCD为矩形，则当点C在
    EF
    上运动时（不与E、F点重合），BD长度的变化情况是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

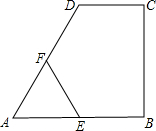    （2012•宜宾）如图，在四边形ABCD中，DC∥AB，CB⊥AB，AB=AD，CD=
    1
    2
    AB，点E、F分别为AB、AD的中点，则△AEF与多边形BCDFE的面积之比为（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•达州）通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．
    原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由．

    （1）思路梳理
    ∵AB=AD，
    ∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．
    ∵∠ADC=∠B=90°，
    ∴∠FDG=180°，点F、D、G共线．
    根据
    SAS
    SAS
    ，易证△AFG≌
    △AEF
    △AEF
    ，得EF=BE+DF．
    （2）类比引申
    如图2，四边形ABCD中，AB=AD，∠BAD=90°点E、F分别在边BC、CD上，∠EAF=45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系
    ∠B+∠D=180°
    ∠B+∠D=180°
    时，仍有EF=BE+DF．
    （3）联想拓展
    如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°．猜想BD、DE、EC应满足的等量关系，并写出推理过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读探究题：如图1，四边形ABCD是正方形（正方形的四边相等，四个角都是直角），点E是边BC的中点．∠AEF=90°，且EF交∠DCG的平分线CF于点F，

    （1）求出角∠ECF的度数？
    （2）求证：AE=EF．
    （3）如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为这样的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．

    查看答案和解析>>

    同步练习册答案