
| 3 |
| 3 |


科目:初中数学 来源: 题型:
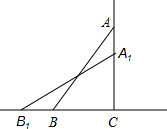 如图,一架13米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为5米,如果梯子的顶端沿墙下滑1米,那么梯子将向外移多少米?(保留两位小数)
如图,一架13米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为5米,如果梯子的顶端沿墙下滑1米,那么梯子将向外移多少米?(保留两位小数)查看答案和解析>>
科目:初中数学 来源: 题型:
 在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.
在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com