
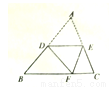
如图,D是AB边上的中点,将△ABC沿过D的直线折健,使点A落住BC上F处,若∠B =50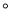 ,则∠ADE= 度.
,则∠ADE= 度.
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册 第1章 丰富的图形世界 单元测试卷 题型:单选题
下列图形不是立体图形的是( )
A. 球 B. 圆柱 C. 圆锥 D. 圆
D 【解析】【解析】 球、圆柱、圆锥均为立体图形,而圆是平面图形,故选D。查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2017-2018学年八年级上学期期末质量检测数学试卷 题型:解答题
在三个整式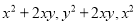 中,请你任意选出两个进行加(或减)运算,使所得整式可以因式分解,并进行因式分解
中,请你任意选出两个进行加(或减)运算,使所得整式可以因式分解,并进行因式分解
查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2017-2018学年八年级上学期期末质量检测数学试卷 题型:单选题
化简: 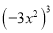 的结果是( )
的结果是( )
A. 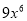 B.
B. 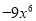 C.
C. 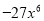 D.
D. 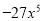
查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城市八年级(上)期末数学试卷(五四学制) 题型:解答题
计算:
(1)(2x+3y)(x﹣y);
(2)(3x2y﹣6xy)÷6xy.
(1)2x2+xy﹣3y2;(2)x﹣1. 【解析】试题分析: (1)按多项式乘以多项式的法则计算即可; (2)按多项式除以单项式的法则计算即可. 试题解析: (1)原式=2x2﹣2xy+3xy﹣3y2=2x2+xy﹣3y2; (2)原式=3x2y÷6xy﹣6xy÷6xy=x﹣1.查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城市八年级(上)期末数学试卷(五四学制) 题型:填空题
科学家发现一种病毒的直径为0.000104米,用科学记数法表示为 米.
1.04× 【解析】由科学记数法知:0.000104=1.04×, 故答案为:1.04×查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城市八年级(上)期末数学试卷(五四学制) 题型:单选题
在代数式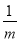 ,
, 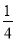 ,
, 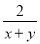 ,a+
,a+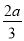 中,分式的个数是( )
中,分式的个数是( )
A. 2 B. 3 C. 4 D. 5
A 【解析】由分式的定义:“形如,其中A、B都是整式,且B中含有字母的式子叫做分式”分析可知,上述各式中: , 属于分式,另外两个式子属于整式. 故选A.查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
【问题提出】已知∠AOB=70°,∠AOD=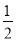 ∠AOC,∠BOD=3∠BOC(∠BOC<45°),求∠BOC的度数.
∠AOC,∠BOD=3∠BOC(∠BOC<45°),求∠BOC的度数.
【问题思考】聪明的小明用分类讨论的方法解决.
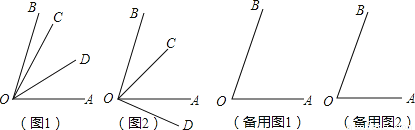
(1)当射线OC在∠AOB的内部时,①若射线OD在∠AOC内部,如图1,可求∠BOC的度数,解答过程如下:
设∠BOC=α,∴∠BOD=3∠BOC=3α,∴∠COD=∠BOD﹣∠BOC=2α,∴∠AOD=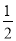 ∠AOC,
∠AOC,
∴∠AOD=∠COD=2α,∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,∴α=14°,∴∠BOC=14°
问:当射线OC在∠AOB的内部时,②若射线OD在∠AOB外部,如图2,请你求出∠BOC的度数;
【问题延伸】(2)当射线OC在∠AOB的外部时,请你画出图形,并求∠BOC的度数.
【问题解决】综上所述:∠BOC的度数分别是 .
查看答案和解析>>
科目:初中数学 来源:浙江省湖州市吴兴区2017-2018学年七年级上学期期终模拟数学试卷 题型:单选题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com