练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列计算结果为的是（ ）

    A. B. C. D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广东深圳助力教育中心2017-2018学年八年级下册数学（北师大版）期末模拟检测卷（1）数学试卷 题型：单选题

    一个平行四边形的两条对角线的长分别为8和10，则这个平行四边形边长不可能是（ ）

    A. 2 B. 5 C. 8 D. 10

    查看答案和解析>>

    科目：初中数学 来源：四川省什邡市2017-2018学年度第二学期八年级数学期末模拟试卷 题型：单选题

    下列描述一次函数y＝－2x＋5的图象及性质错误的是（ ）

    A. y随x的增大而减小 B. 直线经过第一、二、四象限

    C. 当x＞0时，y＜5 D. 直线与x轴交点坐标是（0，5）

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市黄陂区2016~2017学年八年级下学期期末试卷 题型：填空题

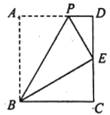
    如图，在矩形ABCD中，点E为CD的中点，点P为AD上一点，沿BP折叠△ABP，点A恰好与点E重合，则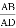的值为___________．

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市黄陂区2016~2017学年八年级下学期期末试卷 题型：单选题

    下图是4×4的正方形网格，每个小正方形的边长为1，每个小正方形的顶点叫格点，点A、B（均在格点上）的位置如图，若以A、B为顶点画面积为2的格点平行四边形，则符合条件的平行四边形的个数有（ ）

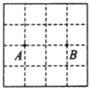
    A. 6 B. 7 C. 9 D. 11

    查看答案和解析>>

    科目：初中数学 来源：安徽省桐城市2017-2018学年八年级下学期期中考试数学试卷 题型：解答题

    勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给

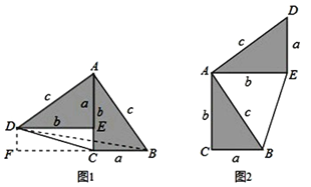
    了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2 ．

    证明：连结DB，过点D作BC边上的高DF，则DF=EC=b﹣a

    ∵S四边形ADCB=S△ACD+S△ABC=b2+ab.

    又∵S四边形ADCB=S△ADB+ S△DCB=c2+a(b-a).

    ∴b2+ab=c2+a(b-a)

    ∴a2+b2=c2

    请参照上述证法，利用图2完成下面的证明．

    将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．求证：a2+b2=c2．

    查看答案和解析>>

    科目：初中数学 来源：安徽省桐城市2017-2018学年八年级下学期期中考试数学试卷 题型：填空题

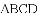
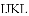
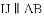
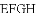
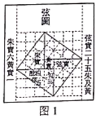
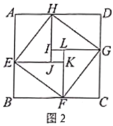
    我国三国时期数学家赵爽为了证明勾股定理，创造了一副“弦图”，后人称其为“赵爽弦图”，如图1所示．在图2中，若正方形的边长为14，正方形的边长为2，且，则正方形的边长为__________．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级(人教版)下学期期末测评卷数学试卷 题型：解答题

    解方程组:

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰州市2018年中考数学试卷 题型：单选题

    下列几何体中，主视图与俯视图不相同的是（　　）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案