练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    用反证法证明一个三角形中不能有两个角是直角的第一步是假设这个三角形中 ________

    有两个角是直角 【解析】用反证法证明一个三角形中不能有两个角是直角时，应先假设这个三角形中有两个角是直角， 故答案为：有两个角是直角．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年湖北省中考数学模拟试卷 题型：填空题

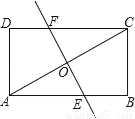
    如图，矩形ABCD中，对角线AC的中点为O，过O作EF⊥AC，分别交AB、DC于E、F，若AB=4，BC=2，那么线段EF的长为_____．

    【解析】如图，连接CE， ∵点O是矩形ABCD对角线AC的中点，EF⊥AC， ∴AE=CE，AO=AC=. 设AE= ，则CE= ，BE= ， 在Rt△BCE中，由勾股定理可得：CE2=BE2+BC2，即， 解得： ，即AE=2.5， ∴在Rt△AOE中，OE=， ∵点O是矩形ABCD对角线AC的中点， ∴点O是矩形的对称中心， ∴EF=2OE...

    查看答案和解析>>

    科目：初中数学 来源：河北省2017-2018学年九年级第一学期第一次月考数学试卷 题型：单选题

    当5个整数从小到大排列，其中位数是4，如果这组数据的唯一众数是6，则5个整数的和最大是（　　）

    A. 21 B. 22 C. 23 D. 24

    A 【解析】由题意知，和最大时这五个整数为2，3，4，6，6，它们的和是21．

    查看答案和解析>>

    科目：初中数学 来源：山东省潍坊高新技术产业开发区2017-2018学年八年级上期末模拟数学试卷 题型：解答题

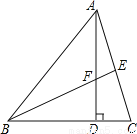
    如图，AD是△ABC的高，BE是△ABC的内角平分线，BE、AD相交于点F，已知∠BAD=40°，求∠BFD的度数．

    65°． 【解析】 试题分析：先根据三角形内角和定理求出∠ABD的度数，再由角平分线的性质求出∠ABF的度数，由三角形外角的性质即可得出结论． 【解析】 ∵AD⊥BC，∠BAD=40°， ∴∠ABD=90°﹣40°=50°． ∵BE是△ABC的内角平分线， ∴∠ABF=∠ABD=25°， ∴∠BFD=∠BAD+∠ABF=40°+25°=65°．

    查看答案和解析>>

    科目：初中数学 来源：山东省潍坊高新技术产业开发区2017-2018学年八年级上期末模拟数学试卷 题型：单选题

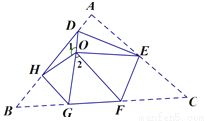
    如右图，将△ABC沿DE、HG、EF翻折，三个顶点均落在点O处，若∠1=129°，则∠2的度数为（   ）

    A. 49° B. 50° C. 51° D. 52°

    C 【解析】根据翻折的性质可知，∠DOE=∠A，∠HOG=∠B，∠EOF=∠C， 又∵∠A+∠B+∠C=180°， ∴∠DOE+∠HOG+∠EOF=180°， ∴∠1+∠2=180°， 又∵∠1=129°， ∴∠2=51°， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：山东省潍坊高新技术产业开发区2017-2018学年八年级上期末模拟数学试卷 题型：填空题

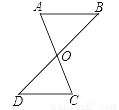
    如图，线段AC、BD相交于点O，且AO=OC，请添加一个条件使△ABO≌△CDO，应添加的条件为________（添加一个条件即可）．

    OB=OD 【解析】在△ABO和△CDO中， ， ∴△ABO≌△CDO（SAS）， 故答案为：OB=OD．

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市莘县2017-2018学年八年级（上）期末模拟数学试卷（含答案） 题型：解答题

    已知y=（m+1）x2﹣|m|+n+4

    （1）当m、n取何值时，y是x的一次函数？

    （2）当m、n取何值时，y是x的正比例函数？

    （1）当m=1，n为任意实数时，这个函数是一次函数； （2）当m=1，n=﹣4时，这个函数是正比例函数． 【解析】试题分析:(1)根据一次函数的定义:形如是y关于x的一次函数关系式,根据自变量x的指数为1和自变量x的系数不能为0,可列方程和不等式求解, (2) 根据正比例函数的定义:形如是y关于x的正比例函数, 根据自变量x的指数为1,和自变量x的系数不能为0,可求出,根据即可求出n....

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市莘县2017-2018学年八年级（上）期末模拟数学试卷（含答案） 题型：单选题

    如果一个三角形两边上的高的交点在三角形的内部，那么这个三角形是（   ）

    A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 任意三角形

    A 【解析】高的交点在三角形内部的是锐角三角形．选A.

    查看答案和解析>>

    科目：初中数学 来源：重庆市2017-2018学年七年级（上）期中数学试卷 题型：解答题

    计算：（1）36﹣27×（）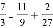

    （2）﹣72+2×（﹣3）2﹣（﹣6）÷（﹣）2．

    （1）4；（2）23. 【解析】试题分析： （1）先用“乘法分配律”将括号去掉，再根据有理数的加、减法法则计算即可； （2）先确定好运算顺序，再按有理数相关运算的运算法则计算即可. 试题解析： （1）原式=； （2）原式=.

    查看答案和解析>>

    同步练习册答案