练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    设a＞b，利用数轴证明|x－a|＋|x－b|的最小值是a－b．

    答案：
    解析：

    　　证∵a＞b∴a与b在数轴上的位置关系如图(1)又∵x为任意实数，∴位于数轴上的情况有3种：即①x位于b点左边(如图(2))，即x＜b②x位于a、b两点之间(如图(3))，即b≤x≤a③x位于a点右边(如图(4))，即x＞a当x＜b时，∵|x－a|＝a－b＋|x－b|∴|x－a|＋|x－b|＝a－b＋2|x－b|＞a－b

    　　当b≤x≤a时，|x－a|＋|x－b|＝a－x＋x－b＝a－b

    　　当x＞a时，∵|x－b|＝a－b＋|x－a|

    　　∴|x－a|＋|x－b|＝a－b＋2|x－a|＞a－b

    　　故综上所述|x－a|＋|x－b|的最小值是a－b


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2012•龙岩）矩形ABCD中，AD=5，AB=3，将矩形ABCD沿某直线折叠，使点A的对应点A′落在线段BC上，再打开得到折痕EF．
    （1）当A′与B重合时，（如图1），EF=
    5
    5
    ；当折痕EF过点D时（如图2），求线段EF的长；
    （2）观察图3和图4，设BA′=x，①当x的取值范围是
    3≤x≤5
    3≤x≤5
    时，四边形AEA′F是菱形；②在①的条件下，利用图4证明四边形AEA′F是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

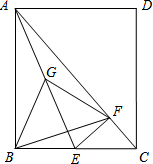    （2013•南平）在矩形ABCD中，点E在BC边上，过E作EF⊥AC于F，G为线段AE的中点，连接BF、FG、GB．设
    ABBC
    =k．
    （1）证明：△BGF是等腰三角形；
    （2）当k为何值时，△BGF是等边三角形？
    （3）我们知道：在一个三角形中，等边所对的角相等；反过来，等角所对的边也相等．事实上，在一个三角形中，较大的边所对的角也较大；反之也成立．
    利用上述结论，探究：当△BGF分别为锐角、直角、钝角三角形时，k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，∠AOB是直角，∠AOC是锐角，ON是∠AOC的角平分线，OM是∠BOC的角平分线；
    （1）如果∠AOC=60°时，∠MON=
    45°
    45°
    ；
    （2）如果∠AOC=50°时，∠MON=
    45°
    45°
    ；
    （3）设∠AOC=x°时，利用你学过的一元一次方程思想，求∠MON的度数．你发现了（证明）一个什么规律？

    查看答案和解析>>

    科目：初中数学 来源：2012年初中毕业升学考试（福建龙岩卷）数学（带解析） 题型：解答题

    矩形ABCD中，AD=5，AB=3，将矩形ABCD沿某直线折叠，使点A的对应点A′落在线段BC上，再打开得到折痕EF．

    （1）当A′与B重合时（如图1），EF=       ；当折痕EF过点D时（如图2），求线段EF的长；
    （2）①观察图3和图4，设BA′=x，①当x的取值范围是       时，四边形AEA′F是菱形；②在①的条件下，利用图4证明四边形AEA′F是菱形．

    查看答案和解析>>

    同步练习册答案