练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列说法正确的是：（ ）

    A．等腰三角形的高、中线、角平分线互相重合

    B．顶角相等的两个等腰三角形全等

    C．等腰三角形一边不可以是另一边的二倍

    D．等腰三角形的两个底角相等

    D． 【解析】 试题分析：A．等腰三角形的高、中线、角平分线互相重合，错误； B．顶角相等的两个三角形全等，错误； C．等腰三角形一边不可以是另一边的二倍，错误， D．等腰三角形的两个底角相等，正确； 故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年秋人教版数学九年级上册 第23章 旋转 全章测试卷 题型：单选题

    在如图所示的四个图案中，既可用旋转来分析整个图案的形成过程，又可用轴对称来分析整个图案的形成过程的图案有( )

    A. 1个 B. 2个 C. 3个 D. 4个

    D 【解析】【解析】 观察四个图形，既是轴对称图形又是中心对称图形，对称中心为四边形的对角线交点，∴四个图形既可用旋转来分析整个图案的形成过程，又可用轴对称来分析整个图案的形成过程．故选D．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.1图形的旋转（1）测试 题型：填空题

    如图，在Rt△ABC中，∠ACB=90°，∠A=α，将△ABC绕点C按顺时针方向旋转后得到△EDC，此时点D在AB边上，则旋转角的大小为______．

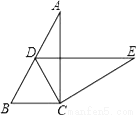
    2a 【解析】试题分析：：∵在Rt△ABC中，∠ACB=90°，∠A=α，∴∠B=90°-α，由旋转的性质可得：CB=CD， ∴∠CDB=∠B=90°-α，∴∠BCD=180°-∠B-∠CDB=2α．即旋转角的大小为2α．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级上册数学第13章13.3《等腰三角形》 题型：填空题

    到三角形各顶点距离相等的点是三角形______________的交点。

    线段中垂线 【解析】到三角形三个顶点的距离相等的点是三角形三边垂直平分线的交点，理由是： ∵P在AB的垂直平分线EF上， ∴， ∵P在AC的垂直平分线MN上， ∴， ∴， 即P是到三角形三个顶点的距离相等的点． 故答案为：线段中垂线.,

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级上册数学第13章13.3《等腰三角形》 题型：填空题

    等腰三角形的一个角是110°，则它的底角是 ．

    35°． 【解析】 试题分析：题中没有指明已知的角是顶角还是底角，故应该分情况进行分析，从而求解． 【解析】 ①当这个角是顶角时，底角=（180°﹣110°）÷2=35°； ②当这个角是底角时，另一个底角为110°，因为110°+110°=240°，不符合三角形内角和定理，所以舍去． 故答案为：35°．

    查看答案和解析>>

    科目：初中数学 来源：贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型：解答题

    口袋中装有四个大小完全相同的小球，把它们分别标号1,2,3,4，从中随机摸出一个球，记下数字后放回，再从中随机摸出一个球，利用树状图或者表格求出两次摸到的小球数和等于4的概率.

    【答案】 .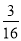

    【解析】试题分析：

    根据题意列表如下，由表可以得到所有的等可能结果，再求出所有结果中，两次所摸到小球的数字之和为4的次数，即可计算得到所求概率.

    试题解析：

    列表如下：

    1

    2

    3

    4

    1

    （1，1）

    （1，2）

    （1，3）

    （1，4）

    2

    （2，1）

    （2，2）

    （2，3）

    （2，4）

    3

    （3，1）

    （3，2）

    （3，3）

    （3，4）

    4

    （4，1）

    （4，2）

    （4，3）

    （4，4）

    由表可知，共有16种等可能事件，其中两次摸到的小球数字之和等于4的有（3，1）、（2，2）和（1，3），共计3种，

    ∴P（两次摸到小球的数字之和等于4）=.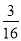

    【题型】解答题
    【结束】
    23

    小亮同学想利用影长测量学校旗杆AB的高度，如图，他在某一时刻立1米长的标杆测得其影长为1.2米，同时旗杆的投影一部分在地面上BD处，另一部分在某一建筑的墙上CD处，分别测得其长度为9.6米和2米，求旗杆AB的高度．

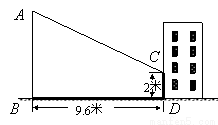
    作DE⊥AB于点E， 根据题意得：， ， 解得：AE=8米． 则AB=AE+BE=8+2=10米． 即旗杆的高度为10米． 【解析】根据同一时刻物高与影长成正比，因而作DE⊥AB于点E，则AE与DE的比值，即同一时刻物高与影长的比值，即可求解．

    查看答案和解析>>

    科目：初中数学 来源：贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型：填空题

    为了估计湖里游多少条鱼，有下列方案：从湖里捕上100条做上标记，然后放回湖里去，经过一段时间，待带标记的鱼完全混合于鱼群后，第二次再捕上200条，若其中带标记的鱼有25条，那么你估计湖里大约有 条鱼.

    【答案】800

    【解析】试题分析：设湖里有鱼x条，由题意得，100÷x=25÷200，解得x=800，所以可以估算湖里有鱼800条．

    故答案为：800．

    考点：一元一次方程的应用．

    【题型】填空题
    【结束】
    16

    如图，在一块长为22 m，宽为17 m的矩形地面上，要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行)，剩余部分种上草坪，使草坪面积为300 m2.若设道路宽为x m，根据题意可列出方程为______________________________．

    (22－x)(17－x)＝300(或x2－39x＋74＝0) 【解析】试题分析：把所修的两条道路分别平移到矩形的最上边和最左边，则剩下的草坪是一个长方形，根据长方形的面积公式列方程．设道路的宽应为x米，由题意有（22﹣x）（17﹣x）=300，故答案为：（22﹣x）（17﹣x）=300．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.3实际问题与二次函数（1）测试 题型：解答题

    如图，在矩形ABCD中，AB=6m，BC=12m，点P从点A出发沿AB边向B以1m/s的速度运动，同时点Q从点B出发，沿BC边向点C以2m/s的速度运动，P、Q两点在分别到达B、C两点后就停止运动，设经过ts时，△PBQ的面积为Sm2，则

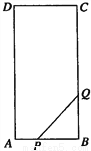
    （1）S与t的函数解析式为：S=_________；

    （2）用表格表示：

    t/s

    1

    2

    3

    4

    5

    6

    7

    8

    9

    S/m2

    （3）用图象表示：

    （4）在这个问题中，自变量t的取值范围是______；图象的对称轴是_______，顶点坐标是________；当t<______时，S的值随t值的增大而_______；当t>______时，S的值随t值的增大而_______（填“增大”或“减小”）；当t=______时，S取得最大值为_______．

    （1）-t2+6（2）填表见解析（3）图像见解析（4）0≤t≤6；t=3；（3，9）；3；增大；3；减小；3；9 【解析】试题分析:(1)根据t秒时,P,Q两点的运动路程,分别表示PB,BQ的长度,可得△BPQ的面积S, (2)把t的值代入解析式可求得对应的S, (3)通过表格,描点,连线即可求解, (4)根据二次函数的图象性质可求解. 试题解析:(1)第t秒时,AP...

    查看答案和解析>>

    科目：初中数学 来源：安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型：解答题

    如图，Rt△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．

    （1）若△BPQ与△ABC相似，求t的值；

    （2）当t为何值时，四边形ACQP的面积最小，最小值是多少？

    （3）连接AQ，CP，若AQ⊥CP，求t的值．

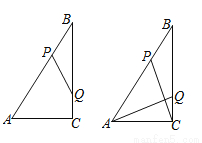
    （1）当t＝1或t＝时；（2）当t=1时，面积最小为18；（3）． 【解析】【试题分析】（1）分类讨论： ，①当△BPQ△BAC时， 则＝，又因为BP＝5t，QC＝4t，AC＝6cm，BC＝8cm， 所以＝，解得：t＝1； ②当△BPQ△BCA时，则＝，即＝，解得：t＝． 综合上述：当t＝1或t＝时，△BPQ与△ABC相似． （2）做PD⊥BC于点D．根据四边形...

    查看答案和解析>>

    同步练习册答案