
 �ڵ�һ�����ཻ�ڵ�C����ACΪб�ߡ���CAOΪ�ڽǵ�ֱ�������Σ�����COΪ�Խ��ߡ�һ����x���ϵľ��������ȣ���C��P����BΪ�����������y=mx2+nx+k�ϣ�ֱ��y=hx+d��˫����y=
�ڵ�һ�����ཻ�ڵ�C����ACΪб�ߡ���CAOΪ�ڽǵ�ֱ�������Σ�����COΪ�Խ��ߡ�һ����x���ϵľ��������ȣ���C��P����BΪ�����������y=mx2+nx+k�ϣ�ֱ��y=hx+d��˫����y= ��������y=ax2+bx+cͬʱ����������ͬ�ĵ�C��D��
��������y=ax2+bx+cͬʱ����������ͬ�ĵ�C��D��
�⣺��1��ֱ�߹���A��B����0=-h+d��1=d����y=x+1��
˫����y= ������C��x1��y1����x1y1=t��
������C��x1��y1����x1y1=t��
��ACΪб�ߣ���CAOΪ�ڽǵ�ֱ�������ε����Ϊ ��y1����1+x1����
��y1����1+x1����
��COΪ�Խ��ߵľ������Ϊx1y�� ��y1����1+x1��=x1y1��
��y1����1+x1��=x1y1��
��Ϊx1��y1��������0���ʵ�x1=1������y1=2�����У� ����t=2��
����t=2��
��2����B��������y=mx2+nx+k�Ķ��㣬
����- ��
��
�õ�n=0��k=1��
��C��������y=mx2+nx+k�ϵĵ㣬
����2=m��1��2+1����m=1��
��3�����P�ĺ�����Ϊp����������Ϊp2+1��
��������y=ax2+bx+c����������ͬ�ĵ�C��D���������D������Ϊ��-2��-1����
��2=a+b+c��
-1=4a-2b+c��
��֮�ã�b=a+1�� c=1-2a��
��y=ax2+�� a+1��x+��1-2a ��
���ǣ�p2+1��ap2+��a+1��p+��1-2a��
������aȡʲôֵ����p2-p�٣�p2+p-2��a��
���ߣ���p2-p=��p2+p-2��a��
��������y=ax2+bx+c������P�㣬
��˷����⣬���н�������⣬
�ʡ�a��0��
���
��֮p=0��p=1������p��1��p��-2.��p=0. ��
����������P����0��1����
�� ��
��
��֮p=1��p=-2������p��0��p��1. ��p=-2��
���������P����-2��5����
����������P����������0��1���ͣ�-2��5����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| t |
| x |
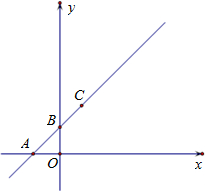 hx+d��˫����y=
hx+d��˫����y=| t |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ֱ��y=hx+d��x���y��ֱ��ཻ�ڵ�A(-1,0),B(0,1),��˫����y=�ڵ�һ�����ཻ�ڵ�C����ACΪб�ߡ�
Ϊ�ڽǵ�ֱ�������Σ�����COΪ�Խ��ߡ�һ����x���ϵľ��������ȣ���C,P����BΪ�����������y=
�ϣ�ֱ��y=hx+d��˫����y=
��������
ͬʱ����������ͬ�ĵ�C��D
��1��ȷ��t��ֵ
��2��ȷ��m , n , k��ֵ
��3��������a , b , c��ֵ����������������P����ȷ��P���꣨12�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010��ȫ���п���ѧ�����ࡶһ�κ�������07���������棩 ���ͣ������
 �ڵ�һ�����ཻ�ڵ�C����ACΪб�ߡ���CAOΪ�ڽǵ�ֱ�������Σ�����COΪ�Խ��ߡ�һ����x���ϵľ��������ȣ���C��P����BΪ�����������y=mx2+nx+k�ϣ�ֱ��y=hx+d��˫����y=
�ڵ�һ�����ཻ�ڵ�C����ACΪб�ߡ���CAOΪ�ڽǵ�ֱ�������Σ�����COΪ�Խ��ߡ�һ����x���ϵľ��������ȣ���C��P����BΪ�����������y=mx2+nx+k�ϣ�ֱ��y=hx+d��˫����y= ��������y=ax2+bx+cͬʱ����������ͬ�ĵ�C��D��
��������y=ax2+bx+cͬʱ����������ͬ�ĵ�C��D��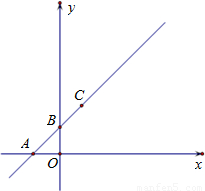
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010����е�ѧУ����ȫ��ͳһ������ѧ�������������� ���ͣ������
��ͼ��ֱ��y=hx+d��x���y��ֱ��ཻ�ڵ�A(-1,0),B(0,1),��˫����y= �ڵ�һ�����ཻ�ڵ�C����ACΪб�ߡ�
�ڵ�һ�����ཻ�ڵ�C����ACΪб�ߡ�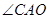 Ϊ�ڽǵ�ֱ�������Σ�����COΪ�Խ��ߡ�һ����x���ϵľ��������ȣ���C,P����BΪ�����������y=
Ϊ�ڽǵ�ֱ�������Σ�����COΪ�Խ��ߡ�һ����x���ϵľ��������ȣ���C,P����BΪ�����������y= �ϣ�ֱ��y=hx+d��˫����y=
�ϣ�ֱ��y=hx+d��˫����y= ��������
�������� ͬʱ����������ͬ�ĵ�C��D
ͬʱ����������ͬ�ĵ�C��D

��1��ȷ��t��ֵ
��2��ȷ��m , n , k��ֵ
��3��������a , b , c��ֵ�������� ��������P����ȷ��P���꣨12�֣�
��������P����ȷ��P���꣨12�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010���Ĵ���������ѧУ��һ��һѧ��������ѧ�� ���ͣ������
��ͼ��ֱ��y=hx+d��x���y��ֱ��ཻ�ڵ�A(-1,0),B(0,1),��˫����y= �ڵ�һ�����ཻ�ڵ�C����ACΪб�ߡ�
�ڵ�һ�����ཻ�ڵ�C����ACΪб�ߡ� Ϊ�ڽǵ�ֱ�������Σ�����COΪ�Խ��ߡ�һ����x���ϵľ��������ȣ���C,P����BΪ�����������y=
Ϊ�ڽǵ�ֱ�������Σ�����COΪ�Խ��ߡ�һ����x���ϵľ��������ȣ���C,P����BΪ�����������y= �ϣ�ֱ��y=hx+d��˫����y=
�ϣ�ֱ��y=hx+d��˫����y= ��������
��������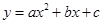 ͬʱ����������ͬ�ĵ�C��D
ͬʱ����������ͬ�ĵ�C��D

��1��ȷ��t��ֵ
��2��ȷ��m , n , k��ֵ
��3��������a , b , c��ֵ��������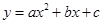 ��������P����ȷ��P���꣨12�֣�
��������P����ȷ��P���꣨12�֣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com