
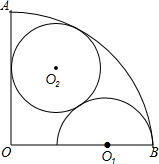
 如图,扇形AOB的半径为3,AO⊥BO,O1是半径OB上一圆心,O1B=1,以O1为圆心,O1B为半径在扇形AOB的形内作半圆O1,又⊙O2与半圆O1外切,与AOI、弧AB都相切.求⊙O2的半径.
如图,扇形AOB的半径为3,AO⊥BO,O1是半径OB上一圆心,O1B=1,以O1为圆心,O1B为半径在扇形AOB的形内作半圆O1,又⊙O2与半圆O1外切,与AOI、弧AB都相切.求⊙O2的半径. 分析 连接O2D、O1 O2,作Q2 M⊥OB于M,连接OC,则OC经过点O2,设⊙O2的半径为x,则OO2=3-x,O1O2=x+1,OM=x,O1M=2-x,在Rt△OO2M和Rt△O1O2M中,由勾股定理得出方程,解方程即可得.
解答 解:如图,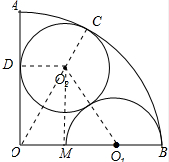 连接O2D、O1 O2,作Q2 M⊥OB于M,连接OC,
连接O2D、O1 O2,作Q2 M⊥OB于M,连接OC,
则OC经过点O2,
设⊙O2的半径为x,
则OO2=3-x,O1O2=x+1,OM=x,O1M=2-x,
在Rt△OO2M和Rt△O1O2M中,
由勾股定理得:OO22-OM2=O1O22-O1M2,
即(3-x)2-x2=(x+1)2-(2-x)2,
解得:x=1,
即O2的半径为1.
点评 本题考查了相切两圆的性质、勾股定理;熟练掌握相切两圆的性质,由勾股定理得出方程是解决问题的关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:选择题
 有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )
有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )| A. | 白 | B. | 红 | C. | 黄 | D. | 黑 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
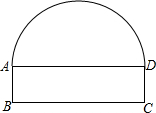 如图,隧道的截面由半圆和长方形构成,长方形的长BC为12m,宽AB为3m,若该隧道内设双行道,现有一辆货运卡车高8m,宽2.3m,则这辆货运卡车能否通过该隧道?
如图,隧道的截面由半圆和长方形构成,长方形的长BC为12m,宽AB为3m,若该隧道内设双行道,现有一辆货运卡车高8m,宽2.3m,则这辆货运卡车能否通过该隧道?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图:A,B,C三点表示的数分别为a,b,c.
如图:A,B,C三点表示的数分别为a,b,c.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com