
 如图,∠AOC=60°,点B在OA上且OB=2
如图,∠AOC=60°,点B在OA上且OB=2 ,若以B为圆心,R为半径的圆与直线OC相离,则R的取值范围是________.
,若以B为圆心,R为半径的圆与直线OC相离,则R的取值范围是________. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (1998•大连)如图,∠AOC=60°,点B在OA上且OB=2
(1998•大连)如图,∠AOC=60°,点B在OA上且OB=2| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
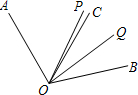 已知如图,∠AOC=60°,∠BOC=50°,OP平分∠AOB,OQ平分∠BOC.
已知如图,∠AOC=60°,∠BOC=50°,OP平分∠AOB,OQ平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
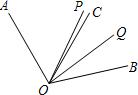 已知如图,∠AOC=60°,∠BOC=50°,OP平分∠AOB,OQ平分∠BOC.
已知如图,∠AOC=60°,∠BOC=50°,OP平分∠AOB,OQ平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,①∠AOC=60°,∠AOB和∠COD都是直角,则∠AOD+∠BOC= ;
②若∠AOC=30°,∠AOB=90°,∠COD=90°,则∠AOD+∠BOC= ;
③∠AOB和∠COD都是直角,试猜想∠AOD和∠BOC这两个角在数量上存在怎样的关系?并说明理由;
④当∠COD绕点O旋转到图(2)的位置,你原来的猜想的结论还正确吗?为什么?
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com