
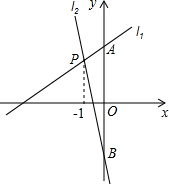 如图,直线l1与l2相交于点P,点P横坐标为-1,l1的解析表达式为y=
如图,直线l1与l2相交于点P,点P横坐标为-1,l1的解析表达式为y= x+3,且l1与y轴交于点A,l2与y轴交于点B,点A与点B恰好关于x轴对称.
x+3,且l1与y轴交于点A,l2与y轴交于点B,点A与点B恰好关于x轴对称. 的点M的坐标;
的点M的坐标; x+3=0+3=3,
x+3=0+3=3, (-1)+3=
(-1)+3= ,
, ),
),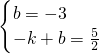 ,
,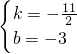 ,
, x-3;
x-3; ,
, ,
, 时,y=(-
时,y=(- )×(-
)×(- )-3=
)-3= -3=-
-3=- ,
, 时,y=(-
时,y=(- )×
)× -3=-
-3=- -3=-
-3=-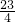 ,
, ,-
,- )或(
)或( ,-
,-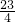 );
); x+3,当y=0时,
x+3,当y=0时, x+3=0,解得x=-6,
x+3=0,解得x=-6, x-3,当y=0时,-
x-3,当y=0时,- x-3=0,
x-3=0,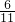 ,
,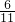 时,l1、l2表示的两个函数的函数值都大于0.
时,l1、l2表示的两个函数的函数值都大于0. 求出点M的横坐标,然后代入直线l2的解析式求解即可;
求出点M的横坐标,然后代入直线l2的解析式求解即可;

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 (2011•裕华区二模)如图,直线l1与l2相交于点P,点P横坐标为-1,l1的解析表达式为y=
(2011•裕华区二模)如图,直线l1与l2相交于点P,点P横坐标为-1,l1的解析表达式为y=| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线l1与l2相交于点P,l1的函数表达式y=kx+b,且经过(1,7)和(-3,-1)两点,点P的横坐标为-1,且l2交y轴于点A(0,-1).
如图,直线l1与l2相交于点P,l1的函数表达式y=kx+b,且经过(1,7)和(-3,-1)两点,点P的横坐标为-1,且l2交y轴于点A(0,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com