
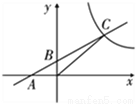
��ͼ��ֱ�� AB ��������ֱ���A(��2��0)��B(0��1)���㣬�뷴����������ͼ���ڵ�һ�����ڵ�C(4��n)����һ�κ����ͷ����������Ľ���ʽ��
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
���x=y����ô���е�ʽ��һ���������ǣ�������
A. x+a=y+a B. x��a=y��a C. ax=ay D. 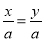
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����������и�����2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
������ʵ֤����������Ⱦ�����̲��ݻ�����ͳ�ƣ�ȫ��ÿ����Լ��14.2�����ˮ���뽭�Ӻ�������14.2���ÿ�ѧ��������ʾΪ��������
A. 1.42��105 B. 1.42��104 C. 142��103 D. 0.142��106
A ��������������������ݿ�ѧ�������ĸ����֪���ÿ�ѧ�������ɽ�һ������ʾ����ʽ�����Խ�14��2���ÿ�ѧ��������ʾ1��42��105,��ѡ��A�� ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ԭ��2018����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
��ͼ���ڿ���Ϊ20m����Ϊ32m�ľ��ε���������ͬ�����ĵ�·��ͼ����Ӱ���֣������µIJ������ϲ�ƺ��Ҫʹ��ƺ�����Ϊ540m2 �� ���·�Ŀ��������С·��Ϊxm���������⣬���з�����ȷ���ǣ� ��
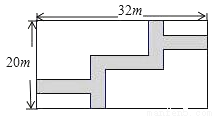
A. ��20+x����32��x��=540 B. ��20��x����32��x��=100
C. ��20��x����32��x��=540 D. ��20+x����32��x��=540
C ���������������� ����ƽ�ƣ�ԭͼ��ת��Ϊ��ͼ����С·��Ϊx�ף���������ã���20��x����32��x��=540����ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ԭ��2018����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
������������y��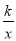 ��ͼ���㣨m��3m��������m��0����˷���������ͼ����������
��ͼ���㣨m��3m��������m��0����˷���������ͼ����������
A. ��һ�������� B. ��һ�������� C. �ڶ��������� D. ������������
B ���������������������m��3m������y=�ã� 3m=�� k=3m2��0�� ��˷�����������ͼ����һ�������ޣ� ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����ػ�ͤ��2017~2018ѧ����꼶��ѧ���ϣ���ĩ���ģ���� ���ͣ������
��ͼ���������� ABCD �У�E ��BC ���е㣬F ��CD ��һ�㣬��CF��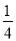 CD�����н��ۣ��١�BAE��30�㣻�ڡ�ABE�ס�ECF����AE��EF���ܡ�ADF�ס�ECF��������ȷ������_____��(�����)
CD�����н��ۣ��١�BAE��30�㣻�ڡ�ABE�ס�ECF����AE��EF���ܡ�ADF�ס�ECF��������ȷ������_____��(�����)
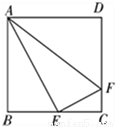
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����ػ�ͤ��2017~2018ѧ����꼶��ѧ���ϣ���ĩ���ģ���� ���ͣ������
��֪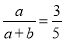 ����
����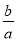 =________��
=________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ��ϰ�����ѧ�Ծ� ���ͣ������
��a=����99��0 ��b=����0.1����1 ��c=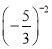 ������������С�����˳����Ϊ________��
������������С�����˳����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�갲��ʡ�����н�������ѧУ�п���ѧģ���Ծ� ���ͣ������
������֤����
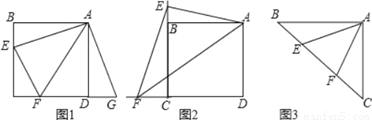
��ͼ1����E��F�ֱ���������ABCD�ı�BC��CD�ϣ���EAF=45�㣬���ж�BE��EF��FD֮���������ϵ��
С�ϰѡ�ABE�Ƶ�A��ʱ����ת90������ADG��ͨ��֤����AEF�ա�AGF���Ӷ����ֲ�֤����EF=BE+FD��
��������
��1����ͼ2����E��F�ֱ���������ABCD�ı�CB��CD���ӳ����ϣ���EAF=45�㣬����EF�������С�ϵķ��ָ������ʾд��EF��BE��DF֮���������ϵ����֤����
��������չ��
��2����ͼ3����ͼ����BAC=90�㣬AB=AC����E��F�ڱ�BC�ϣ��ҡ�EAF=45�㣬��BE=3��EF=5����CF�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com