练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1），B（﹣1，4），C（﹣3，3）．

    （1）画出△ABC关于y轴对称的△A1B1C1，并写出A1点的坐标及sin∠B1A1C1的值；

    （2）以原点O为位似中心，位似比为1：2，在y轴的左侧，画出 将△ABC放大后的△A2B2C2，并写出A2点的坐标；

    （3）若点D（a，b）在线段AB上，直接写出经过（2）的变化后点D的对应点D2的坐标．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：吉林省2018年中考数学全真模拟试卷 题型：填空题

    一个多边形的内角和是外角和的2倍，则这个多边形的边数为_____．

    查看答案和解析>>

    科目：初中数学 来源：2018年山东省济南市天桥区初三下学期数学一模试卷 题型：解答题

    【探索发现】

    如图①，是一张直角三角形纸片，∠B=90°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大，随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为　 　．

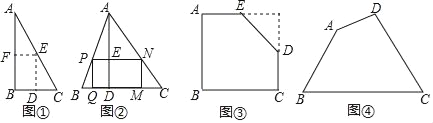
    【拓展应用】

    如图②，在△ABC中，BC=a，BC边上的高AD=h，矩形PQMN的顶点P、N分别在边AB、AC上，顶点Q、M在边BC上，则矩形PQMN面积的最大值为　 　．（用含a，h的代数式表示）

    【灵活应用】

    如图③，有一块“缺角矩形”ABCDE，AB=32，BC=40，AE=20，CD=16，小明从中剪出了一个面积最大的矩形（∠B为所剪出矩形的内角），求该矩形的面积．

    【实际应用】

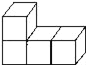
    如图④，现有一块四边形的木板余料ABCD，经测量AB=50cm，BC=108cm，CD=60cm，且tanB=tanC=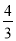，木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN，求该矩形的面积．

    查看答案和解析>>

    科目：初中数学 来源：2018年山东省济南市天桥区初三下学期数学一模试卷 题型：单选题

    解分式方程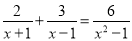，分以下四步，其中，错误的一步是( )

    A. 方程两边分式的最简公分母是（x–1）（x+1）

    B. 方程两边都乘以（x–1）（x+1），得整式方程2（x–1）+3（x+1）=6

    C. 解这个整式方程，得x=1

    D. 原方程的解为x=1

    查看答案和解析>>

    科目：初中数学 来源：2018年山东省济南市天桥区初三下学期数学一模试卷 题型：单选题

    如图，下列几何体是由4个相同的小正方体组合而成的，从左面看得到的平面图形是下列选项中的（　　）

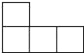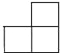    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源：吉林省名校2017-2018学年调研系列卷九年级（上）期中数学试卷 题型：解答题

    已知关于x的一元二次方程kx2+2x﹣1=0有实数根，

    （1）求k的取值范围；

    （2）当k=2时，请用配方法解此方程．

    查看答案和解析>>

    科目：初中数学 来源：吉林省名校2017-2018学年调研系列卷九年级（上）期中数学试卷 题型：填空题

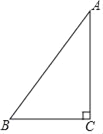
    如图，已知在Rt△ABC中，∠C=90°，AB=5，BC=3，则cosB的值是_____．

    查看答案和解析>>

    科目：初中数学 来源：广西贵港市港南区2018年中考数学一模试卷 题型：填空题

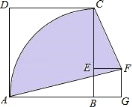
    如图，正方形ABCD的面积为36cm2，点E在BC上，点G在AB的延长线上，四边形EFGB是正方形，以点B为圆心，BC的长为半径画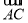，连接AF，CF，则图中阴影部分的面积为_____．

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级数学下册：5.3平行线的性质同步练习 题型：解答题

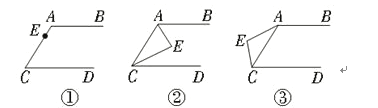
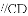
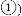
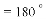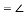
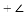
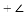
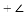
    如图，已知AB ，在AB，CD之间取一点E，连接EA，EC，试探索 AEC与 EAB， ECD之间的关系若点E取在AC上如图，则 AEC，由此可得 AEC EAB ECD或 AEC EAB ECD如果点E取在AC的两侧如图，结论会是什么？

    查看答案和解析>>

    同步练习册答案