
如图,E,D分别是AB,AC上的点,∠EBC与∠BCD的平分线交于M,∠BED与∠EDC的平分线交于N.试探究:A,M,N三点有什么样的位置关系,并证明你探究的结论.

|
A,M,N三点共线. 证明:作NF⊥AB,NG⊥ED,NH⊥AC,垂足分别为F,G,H. ∵NE,ND分别是∠BED,∠CDE的平分线, ∴NF=NG,NG=NH,∴NF=NH. ∴点N在∠A的角平分线上. 又∵MB是∠ABC的平分线,MC是∠ACB的平分线,∴点M在∠A的平分线上. 因此,A,M,N三点共线. 剖析:探究A,M,N三点的位置关系,要么A,M,N三点共线;要么A,M,N三点不共线.由观察图形可直观得出A,M,N三点共线,根据题设条件和三角形三条角平分线交于一点,点M在∠A的平分线上,问题转化为证点N在∠A的平分线上即可.根据平分线的性质定理和判定定理,作NF⊥AB,NG⊥ED,NH⊥AC,不难证得结果. |
|
方法提炼: 证三点共线问题,一是证明其邻角互补,即连接AM,MN,证∠AMB+∠BMN= |


科目:初中数学 来源: 题型:
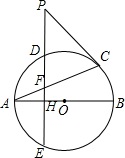 如图:AB、AC分别是⊙O的直径和弦,D为弧AC上一点,DE⊥AB于点H,交⊙O于点E,交AC于点F.P为ED延长线上一点,连PC.
如图:AB、AC分别是⊙O的直径和弦,D为弧AC上一点,DE⊥AB于点H,交⊙O于点E,交AC于点F.P为ED延长线上一点,连PC.| BC |
| AB |
| 3 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com