Question

四边形ABCD的对角线AC、BD的长分别为m、n．
（1）当AC⊥BD时（如图1），请证明，四边形ABCD的面积；
（2）当AC、BD所夹的锐角为θ时（如图2），猜想四边形ABCD的面积S与m、n、θ的关系，并证明．

Answer 1

（1）证明：如图1，AC与BD的垂足为O点，
∵AC⊥BD，
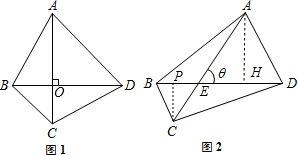
∴S_△ABD=AO•BD，S_△CBD=CO•BD，
∴四边形ABCD的面积=S_△ABD+S_△CBD=AO•BD+CO•BD=BD•（AO+CO）=BD•AC=mn；

（2）解：作AH⊥BD于H点，CP⊥BD于P点，AC与BD交于E点，如图2，
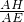在RtAEH中，sinθ=，即AH=AE•sinθ，
在RtCPE中，sin∠PEC=，PC=CE•sin∠PEC=CE•sinθ，
∵S_△ABD=AH•BD，S_△CBD=CP•BD，
∴四边形ABCD的面积S=S_△ABD+S_△CBD=AH•BD+CP•BD=AE•sinθ•BD+CE•sinθ•BD=BD•（AE+CE）•sinθ=BD•AC•sinθ=m•n•sinθ．
分析：（1）根据三角形面积公式得到S_△ABD=AO•BD，S_△CBD=CO•BD，然后把两个三角形面积相加即可得到结论；
（2）作AH⊥BD于H点，CP⊥BD于P点，AC与BD交于E点，根据正弦的定义得到AH=AE•sinθ，PC=CE•sin∠PEC=CE•sinθ，然后再根据三角形面积公式得到S_△ABD=AH•BD，S_△CBD=CP•BD，再把两个三角形面积相加即可得到四边形ABCD的面积S=m•n•sinθ．
点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．也考查了三角形面积公式．