
如图,在平面直角坐标系中,O为坐标原点,直线y=﹣x﹣3与x轴交于点A,与y轴交于点C,抛物线y=x2+bx+c经过A、C两点,与x轴交于另一点B
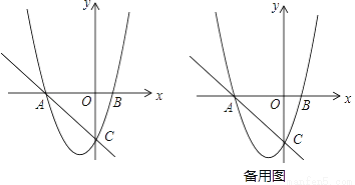
(1)求抛物线的解析式;
(2)点D是第二象限抛物线上的一个动点,连接AD、BD、CD,当S△ACD=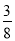 S四边形ACBD时,求D点坐标;
S四边形ACBD时,求D点坐标;
(3)在(2)的条件下,连接BC,过点D作DE⊥BC,交CB的延长线于点E,点P是第三象限抛物线上的一个动点,点P关于点B的对称点为点Q,连接QE,延长QE与抛物线在A、D之间的部分交于一点F,当∠DEF+∠BPC=∠DBE时,求EF的长.
(1)y=x2+2x﹣3(2)(﹣4,5)(3)3+ 【解析】试题分析:(1)、首先求出点A和点C的坐标,然后将其代入二次函数解析式,利用待定系数法求出函数解析式;(2)、首先求出AB的长度,然后根据面积之间的关系得出点E的坐标,从而得出直线CE的函数解析式,将一次函数和二次函数联立成方程组,从而得出点D的坐标;(3)、过点D作DN⊥x轴,垂足为N,过点P作PM⊥x轴,垂足为M,利用待定系数... 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第4章 图形的相似 单元测试卷 题型:单选题
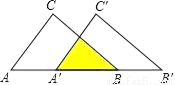
如图:把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半,若AB= ,则此三角形移动的距离AA′是( )
,则此三角形移动的距离AA′是( )
A.  -1 B.
-1 B. 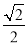 C. 1 D.
C. 1 D. 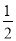
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第12章 全等三角形 单元测试 题型:单选题
如图,△AOC≌△BOD,点A与点B是对应点,那么下列结论中错误的是( )
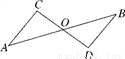
A. ∠A=∠B B. AO=BO C. AB=CD D. AC=BD
C 【解析】试题解析:∵△AOC≌△BOD, ∴∠A=∠B,AO=BO,AC=BD, ∴A、B. D均正确, 而AB、CD不是不是对应边,∴AB≠CD, 故选C.查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期七年级期末质量检测数学试卷 题型:填空题
比较大小, 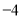 ______
______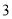 (用“>”,“<”或“=”填空).
(用“>”,“<”或“=”填空).
查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期七年级期末质量检测数学试卷 题型:单选题
在下列变形中,正确的是( )
A. 如果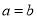 ,那么
,那么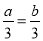 B. 如果
B. 如果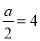 ,那么
,那么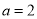
C. 如果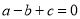 ,那么
,那么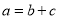 D. 如果
D. 如果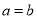 ,那么
,那么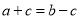
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学 第二章 二次函数 单元检测卷 题型:填空题
已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:则当2<y<5时,x的取值范围是________
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 10 | 5 | 2 | 1 | 2 | … |
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学 第二章 二次函数 单元检测卷 题型:填空题
如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a﹣2b+c的值为________.
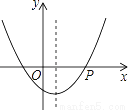
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第一章整式乘法1.2幂的乘方与积的乘方课时练习 题型:解答题
若x3 =8a3b6,求x的值
2ab2 【解析】试题分析:根据积的乘方法则可完成此题. 试题解析:8a3b6=(2ab2)3 , ∵x3 =8a3b6, ∴x的值为2ab2查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第2章 一元二次方程 单元测试卷 题型:单选题
一个等腰三角形的两边长分别是方程x2-7x+10=0的两根,则该等腰三角形的周长是( )
A. 12 B. 9 C. 13 D. 12或9
A 【解析】试题分析:因式分解可得:(x-2)(x-5)=0,解得: =2, =5.当2为底,5为腰时,则三角形的周长为12;当5为底,2为腰时,则无法构成三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com