
求证:等腰梯形的四个顶点在同一个圆上.
已知:四边形ABCD是等腰梯形,AB=CD,AD∥BC.
求证:A、B、C、D在同一个圆上.
|
解:如下图作AB的垂直平分线l1,作BC的垂直平分线l2, ∵AB与BC相交, ∴l1与l2必相交,设交点O,∵O在l1上,∴OA=OB. 又O在l2上,∴OB=OC. ∵等腰梯形是轴对称图形,l2为BC的垂直平分线, ∴l2为等腰梯形ABCD的对称轴,∴OA=OD, ∴OA=OB=OC=OD, ∴A、B、C、D在以O为圆心的圆上.
思路点拨:要证明A、B、C、D在同一个圆上,根据圆的定义只要找到O点,使得A、B、C、D到O点的距离相等.我们由前面的知识可知,到A、B距离相等的点在AB的垂直平分线上,因此,只需作出AB与BC的垂直平分线即可. 评注:本题的关键是找出O点,然后根据以前学过的知识证明OA=OB=OC=OD,除了分别作出AB与BC的中垂线之外,也可分别作出AB与CD的中垂线,它们也相交于O点,并且证明OA=OB=OC=OD时,上述证明方法中用了轴对称图形的性质,也可以利用全等三角形的方法证明. 小结:证明几个点共圆的方法. (1)要证明几个点在同一个圆上,可以根据定义,证明这几个点与一个定点距离相等. 注意:这个定点可能是已知的,也可能是未知的,可以通过作中垂线等方法找到它. (2)证明五点共圆是先证三个点确定一个圆,然后再证第4个点和第5个点均在这个圆上. |


科目:初中数学 来源: 题型:
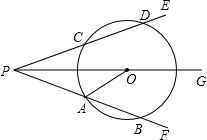 ∠EPF的两边相交于A、B和C、D,连接OA,此时有OA∥PE.
∠EPF的两边相交于A、B和C、D,连接OA,此时有OA∥PE.| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
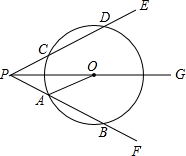 (2012•樊城区模拟)如图,O为∠EPF内射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A,B和C,D且AB=CD,连接OA,此时有OA∥PE.
(2012•樊城区模拟)如图,O为∠EPF内射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A,B和C,D且AB=CD,连接OA,此时有OA∥PE.查看答案和解析>>
科目:初中数学 来源: 题型:
(本题8分)如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF 的两边相交于A、B和C、D,连结OA,此时有OA//PE.
(1)求证:AP=AO;
(2)若tan∠OPB=![]() ,求弦AB的长;
,求弦AB的长;
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为 ▲ ,能构成等腰梯形的四个点为 ▲ 或 ▲ 或 ▲ .
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(山东烟台卷)数学 题型:解答题
(2011•金华)如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF的两边相交于A、B和C、D,连接OA,此时有OA∥PE.
(1)求证:AP=AO;
(2)若tan∠OPB=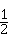 ,求弦AB的长;
,求弦AB的长;
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为_________,能构成等腰梯形的四个点为__________或__________或___________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com