解(1)作CN⊥AB,交GF于点M,交AB于点N.

在Rt△ABC中,
∵AC=4,BC=3,
∴AB=5,
∴

AB•CN=

AC•BC,
∴CN=

=

,
∵GF∥AB,
∴△CGF∽△CAB,
∴
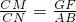
,

设每个正方形边长为x,则

,
∴x=

;
(2)解:如右图所示,
根据条件可以得到△DKE∽△EPF,
∴DK:PE=KE:PF,
而DK=m-n,FG=c,PE=n-c,PF=c,
∴(m-n):(n-c)=n:c,
∴n
2=mc,
∴正方形HPFG的边长是
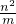
.
分析:(1)设每个正方形边长为x,首先根据面积定值求出三角形ACB斜边上的高线长,作CN⊥AB,交GF于点M,交AB于点N,因为△CGF∽△CAB,根据对应边的比等于相似比可求出正方形的边长.
(2)设正方形HPFG的边长为c,根据相似三角形的性质,对应边的比相等可得m,n和c的关系.
点评:本题考查了正方形的性质,相似三角形的判定与性质,解题的关键是根据相似三角形对应边成比例找出后面正方形的边长与第一个正方形的边长的关系.



 AB•CN=
AB•CN= AC•BC,
AC•BC, =
= ,
,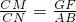 ,
,
 ,
, ;
;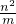 .
.

 名校课堂系列答案
名校课堂系列答案