练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列函数中,自变量的取值范围为x≥3的是（ ）。

    A. B. C. D.

    B 【解析】A、； B、； C、； D、； 故选B。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市校2018届九年级上学期期末模拟数学试卷 题型：单选题

    抛物线y=的顶点坐标是（ ）.

    A．（3，5） B．（﹣3，5） C．（3，﹣5） D．（﹣3，﹣5）

    B． 【解析】 试题分析：由抛物线的解析式可求得答案．∵y=，∴抛物线顶点坐标为（﹣3，5）. 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：江苏省东台市2017-2018学年上学期期末考试九年级数学试卷 题型：填空题

    如图，AB，AC分别是☉O的直径和弦，OD⊥AC于点D，连接BD，BC，AB=5，AC=4，则BD=____. 

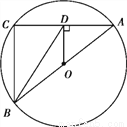
    【解析】∵AB是⊙O的直径， ∴∠ACB=90°， 又∵AB=5，AC=4，OD⊥AC于点D， ∴BC=，CD=AC=2， ∴BD=. 即答案为.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：解答题

    已知x=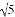+3，y=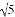﹣3，求下列各式的值：

    （1）x2﹣2xy+y2 ；（2）x2﹣y2．

    （1）36；（2）12 【解析】试题分析：先由条件求出：x+y=2，x-y=6；再把结论进行变形，代入求值即可. 试题解析：∵x=+3, y=-3 ∴x+y=2，x-y=6 (1)x2-2xy+y2=(x+y)2=(2)2="20," (2)x2-y2="(x+y)(x-y)=" 2×6=12.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：填空题

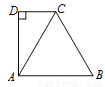
    如图，△ABC为等边三角形，DC∥AB，AD⊥CD于D．若△ABC的周长为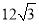cm，则

    CD =________________cm．

    【解析】试题解析：∵等边△ABC的周长为cm， ∴AC=12÷3=4cm，∠BAC=60°， ∵DC∥AB， ∴∠ACD=∠BCA=60°， ∵AD⊥CD， ∴∠CAD=90°-∠ACD=90°-60°=30°， ∴CD=AC=×4=2cm．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：单选题

    如图，在平面直角坐标系xOy中，等腰梯形ABCD的顶点坐标分别为A（1，1），B（2，﹣1），C（﹣2，﹣1），D（﹣1，1）．y轴上一点P（0，2）绕点A旋转180°得点P1 ，点P1绕点B旋转180°得点P2 ，点P2绕点C旋转180°得点P3 ，点P3绕点D旋转180°得点P4 ，…，重复操作依次得到点P1 ，P2 ，…，则点P2010的坐标是（　　）

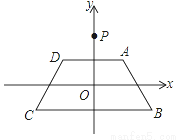
    A. （2010，2） B. （2012，﹣2 ） C. （0，2） D. （2010，﹣2 ）

    D 【解析】由已知可以得到，点P1，P2的坐标分别为（2，0），（2，﹣2）， 记P2（a2 ，b2），其中a2=2，b2=﹣2， 根据对称关系，依次可以求得：P3（﹣4﹣a2，﹣2﹣b2），P4（2+a2， 4+b2），P5（﹣a2 ，﹣2﹣b2），P6（4+a2，b2）， 令P6（a6，b2）， 同样可以求得，点P10的坐标为（4+a6，b2），即P10（4×2+...

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：解答题

    在创建全国森林城市的活动中，我区一“青年突击队”决定义务整修一条1000米长的绿化带，开工后，附近居民主动参加到义务劳动中，使整修的速度比原计划提高了一倍，结果提前4小时完成任务，问“青年突击队”原计划每小时整修多少米长的绿化带？

    原计划每小时整修125米长的绿化带． 【解析】试题分析：设原计划每小时整修x米长的绿化带，根据“计划时间-实际时间=4”这一等量关系列出方程，解方程即可得. 试题解析：设原计划每小时整修x米长的绿化带， 根据题意得： ， 解得：x=125， 经检验：x=125是原方程的解， ∴x=125 答：原计划每小时整修125米长的绿化带．

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：单选题

    满足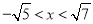的整数x有（     ）个

    A. 6个 B. 5个 C. 4个 D. 3个

    B 【解析】【解析】 由题意得： ＜≤x≤＜，∴满足条件的整数有-2，-1，0，1，2，共5个．故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型：解答题

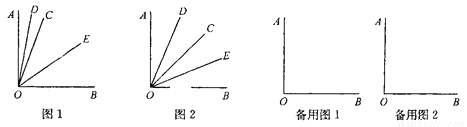
    已知∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD，OE．

    (1) 如图1，当∠BOC=70°时，求∠DOE的度数．

    (2) 如图2，当射线OC在∠AOB内绕点O旋转时，∠DOE的大小是否发生变化?说明理由．

    (3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时，画出图形，直接写出相应的∠DOE的度数．(不必写出过程)

    (1)45°;(2)45°;(3) ∠DOE的大小发生变化.45°或135°. 【解析】试题分析： （1）因为∠DOE=∠COD+∠COE，所以分别根据角平分线的定义求出∠COD和∠COE即可； （2）因为∠DOE=∠COD+∠COE，结合角平分线即可求解； （3）需要分类，当∠AOC是钝角时和当∠AOC大于钝角时，结合角平分线求解. 试题解析： (1) 根据题...

    查看答案和解析>>

    同步练习册答案