练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若5x2m y2和-7x6 yn是同类项，则m +n=_______ .

    5 【解析】试题解析：根据同类项的定义得： 解得： 故答案为：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年山东省枣庄市中考数学模拟试卷 题型：单选题

    如图，AB、AC是⊙O的两条弦，∠A=25°，过点C的切线与OB的延长线交于点D，则∠D的度数（ ）

    A．25° B．30° C．40° D．50°

    C． 【解析】 试题分析：连接OC，∵CD是切线，∴∠OCD=90°， ∵∠A=25°， ∴∠COD=2∠A=50°， ∴∠D=90°﹣50°=40°． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省武汉市中考数学模拟试卷二 题型：解答题

    把下列各数填在相应的表示集合的大括号里：

    2，﹣3，﹣1.5，0，π，﹣0.3

    （1）非正整数集合{　 　…}

    （2）正数集合{　 　…}

    （3）非正有理数集合{　 　…}

    （4）负分数集合{　 　…}

    （5）有理数集合{　 　…}．

    答案见解析. 【解析】试题分析：根据题目中的数据和题意，可以将题目中的数据写入不同的集合中，本题得以解决． 试题解析：在2，﹣3，﹣1.5，0，π，﹣0.3中， （1）非正整数集合{﹣3，0，…} （2）正数集合{2，π，…} （3）非正有理数集合{﹣3，﹣1.5，0，﹣0.3，…} （4）负分数集合{﹣1.5，﹣0.3，…} （5）有理数集合{2，﹣3，...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省武汉市中考数学模拟试卷二 题型：单选题

    在，﹣（﹣2）2，|﹣2.5|，0，3﹣π，15%中，非负数的个数为（　　）

    A. 2 B. 3 C. 4 D. 5

    C 【解析】是非负数，﹣（﹣2）2=-4是负数，|﹣2.5|=2.5是非负数，0是非负数，3﹣π是负数，15%是非负数，所以非负数共有4个. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型：解答题

    先化简，后求值： ，其中.

    3 【解析】试题分析：先去括号，再合并同类项，代入数值计算即可. 试题解析：原式 当时， 原式=.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型：填空题

    海中一潜艇所在高度为-30米，此时观察到海底一动物位于潜艇的正下方30米处，则海底动物的高度为___________．

    -60米 【解析】试题解析：?30?30=(?30)+(?30)=?60（米）. 故答案为：?60米.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型：单选题

    在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为（　　）

    A. 69° B. 111° C. 141° D. 159°

    C 【解析】试题分析：首先计算出∠3的度数，再计算∠AOB的度数即可． 【解析】 由题意得：∠1=54°，∠2=15°， ∠3=90°﹣54°=36°， ∠AOB=36°+90°+15°=141°， 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：填空题

    如图，⊙O中，弦AB=3，半径BO=，C是AB上一点且AC=1，点P是⊙O上一动点，连PC，则PC长的最小值是_______

    【解析】试题解析：过点O作OD⊥AB于点D，连接OP、OC， ∵AB=3， ∴由垂径定理可知： ∴由勾股定理可知： ∵AC=1， ∴由勾股定理可知：OC=1， 在△OCP中，由三角形三边关系可知： PC>OP?OC， ∴当O、C.P三点共线时，PC可取得最小值， 此时 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：解答题

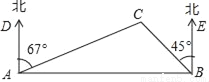
    一艘救生船在码头A接到小岛C处一艘渔船的求救信号，立即出发，沿北偏东67°方向航行10海里到达小岛C处，将人员撤离到码头A张东方向的码头B，测得小岛C位于码头B西北方向，求码头B与小岛C的距离（结果精确到0.1海里）．【参考数据：sin23°=0.39，cos23°=0.92，tan23°=0.42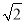， =1.41】

    5.5海里 【解析】试题分析：本题考查了解直角三角形的应用---方向角问题，作CD⊥AB，在Rt△ADC中由sin23°= ,求得CD=3.9，在Rt△BCD中由sin45°= ,求得BC=CD，即可得出答案． 【解析】 过点C作CD⊥AB于点D， 由题意，得：∠BAC=23°，∠ABC=45°，AC=10， 在Rt△ADC中，∠ADC=90°， ∴sin23°==...

    查看答案和解析>>

    同步练习册答案