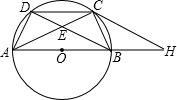
证明:(1)∵C为劣弧BD的中点,
∴

=

,
∴∠DAC=∠BAC,
又∠DAC和∠BDC对的弧都为

,
∴∠DAC=∠BDC.
∴∠BAC=∠BDC,又∠DCA=∠DCA,
∴△DEC∽△ADC.
(2)由(1)知,△DEC∽△ADC,
∴EC:DC=DC:AC.
∴DC
2=3,DC=

=BC.
∵AB是直径,
∴∠ACB=90°.
在Rt△BCE中,CE=1,BC=

,
∴BE=2,
∴∠CBE=30°,
∴∠BAC=∠DAC=30°.
∴劣弧BD的度数为2×2×30°=120°,劣弧AD的度数为60°.
即∠DCA=30°=∠CAB.
∴CD∥AB,且CD≠AB.
∴四边形ABCD是上底为DC,下底为AB,高为直角三角形斜边AB边上的高的梯形.
∵AC=AE+EC=3,BC=

,根据勾股定理得AB=2

,则∠CAB=30°,
∴直角三角形斜边AB边上的高为

,
∴S
梯形ABCD=
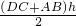
=
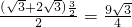
.
分析:(1)根据圆周角定理,同弧所对的圆周角相等易得∠DAC=∠BDC,再由C是劣弧BD的中点,得到

=

,根据等弧所对的圆周角也相等可得∠DAC=∠CAB,等量代换可得三个角都相等,同时又有∠DCA=∠DCA,易得出证明;
(2)根据题意易得DC
2=3,DC=

=BC,进而可得劣弧BD、AD的度数;即∠DCA=∠CAB,可得CD∥AB,且CD≠AB,可判断得出四边形ABCD是梯形.
点评:本题考查垂弦定理、圆心角、圆周角的应用能力和相似三角形的判定和性质的应用.

 .
. =
= ,
, ,
, =BC.
=BC. ,
, ,根据勾股定理得AB=2
,根据勾股定理得AB=2 ,则∠CAB=30°,
,则∠CAB=30°, ,
,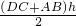 =
=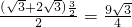 .
. =
= ,根据等弧所对的圆周角也相等可得∠DAC=∠CAB,等量代换可得三个角都相等,同时又有∠DCA=∠DCA,易得出证明;
,根据等弧所对的圆周角也相等可得∠DAC=∠CAB,等量代换可得三个角都相等,同时又有∠DCA=∠DCA,易得出证明; =BC,进而可得劣弧BD、AD的度数;即∠DCA=∠CAB,可得CD∥AB,且CD≠AB,可判断得出四边形ABCD是梯形.
=BC,进而可得劣弧BD、AD的度数;即∠DCA=∠CAB,可得CD∥AB,且CD≠AB,可判断得出四边形ABCD是梯形.

 口算题天天练系列答案
口算题天天练系列答案 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°. 如图,点A的坐标为(2
如图,点A的坐标为(2