
 在边长为1的正方形ABCD的边AB上取一点P,边BC上取一点Q,边CD上取一点M,边AD上取一点N,如果AP+AN+CQ+CM=2,求证:PM⊥QN.
在边长为1的正方形ABCD的边AB上取一点P,边BC上取一点Q,边CD上取一点M,边AD上取一点N,如果AP+AN+CQ+CM=2,求证:PM⊥QN.

科目:初中数学 来源: 题型:
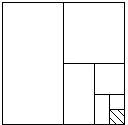 我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.
在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com