
 与x轴交于A、B(A在B左侧),顶点为C(1,﹣2)。
与x轴交于A、B(A在B左侧),顶点为C(1,﹣2)。
解:(1)∵抛物线y= x2+bx+c的顶点为C(1,﹣2), x2+bx+c的顶点为C(1,﹣2),∴﹣  =﹣ =﹣ =1, =1,解得b=﹣1,  = = =﹣2, =﹣2,解得c=﹣  , ,∴抛物线解析式为y=  x2﹣x﹣ x2﹣x﹣ , ,令y=0,则  x2﹣x﹣ x2﹣x﹣ =0, =0,解得x1=﹣1,x2=3, ∴点A、B的坐标为:A(﹣1,0)、B(3,0); (2)∵A(﹣1,0)、B(3,0)、C(1,﹣2), ∴AB=3﹣(﹣1)=4,AC=  =2 =2 , ,BC=  =2 =2 , ,∴AB2=16,AC2+BC2=8+8=16, ∴AB2=AC2+BC2, ∴△ABC是直角三角形,AB是直径,故半径为2; (3)①当AB是平行四边形的边时,PE=AB=4,且点P、E的纵坐标相等, ∴点P的横坐标为4或﹣4, ∴y=  ×42﹣4﹣ ×42﹣4﹣ = = , ,或y=  ×42+4﹣ ×42+4﹣ = = , ,∴点P、E的坐标为P1(4,  )、E1(0, )、E1(0, )或P2(﹣4, )或P2(﹣4, )、E2(0, )、E2(0, ), ),②如图,当AB是平行四边形的对角线时,PE平分AB, ∴PE与x轴的交点坐标D(1,0), 过点E作EF⊥AB,则OD=FD, ∴点F的坐标为(2,0), ∴点P的横坐标为2,y=  ×22﹣2﹣ ×22﹣2﹣ =﹣ =﹣ , ,∴点P的纵坐标为  , ,∴点P、E的坐标为P3(2,﹣  )、E3(0, )、E3(0, ), ),综上所述,点P、E的坐标为:P1(4,  )、E1(0, )、E1(0, )或P2(﹣4, )或P2(﹣4, )、E2(0, )、E2(0, )或P3(2,﹣ )或P3(2,﹣ )、E3(0, )、E3(0, )。 )。 |
 |


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
如图,抛物线:![]() 与x轴交于A、B(A在B左侧),顶点为C(1,-2),
与x轴交于A、B(A在B左侧),顶点为C(1,-2),

1.求此抛物线的关系式;并直接写出点A、B的坐标
2.求过A、B、C三点的圆的半径.
3.在抛物线上找点P,在y轴上找点E,使以A、B、P、E为顶点的四边形是平行四边形,求点P、E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线:![]() 与x轴交于A、B(A在B左侧),顶点为C(1,-2),
与x轴交于A、B(A在B左侧),顶点为C(1,-2),

1.(1)求此抛物线的关系式;并直接写出点A、B的坐标.
2.(2)求过A、B、C三点的圆的半径.
3.(3)在抛物线上找点P,在y轴上找点E,使以A、B、P、E为顶点的四边形是平行四边形,求点P、E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
 与x轴交于A、B(A在B左侧),顶点为C(1,-2),
与x轴交于A、B(A在B左侧),顶点为C(1,-2),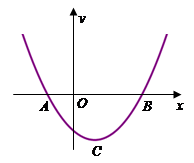
查看答案和解析>>
科目:初中数学 来源:2012届浙江省临海市灵江中学九年级2月月考数学卷 题型:解答题
如图,抛物线: 与x轴交于A、B(A在B左侧),顶点为C(1,-2),
与x轴交于A、B(A在B左侧),顶点为C(1,-2),
【小题1】(1)求此抛物线的关系式;并直接写出点A、B的坐标.
【小题2】(2)求过A、B、C三点的圆的半径.
【小题3】(3)在抛物线上找点P,在y轴上找点E,使以A、B、P、E为顶点的四边形是平行四边形,求点P、E的坐标.
查看答案和解析>>
科目:初中数学 来源:2013年广东省东莞市中考数学模拟试卷(五)(解析版) 题型:解答题
 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com