
 x+
x+ 与直线l2:y=﹣2x+16相交于点C,l1、l2分别交x轴于A、B两点.矩形DEFG的顶点D、E分别在直线l1、l2上,顶点F、G都在x轴上,且点G与点B重合.
与直线l2:y=﹣2x+16相交于点C,l1、l2分别交x轴于A、B两点.矩形DEFG的顶点D、E分别在直线l1、l2上,顶点F、G都在x轴上,且点G与点B重合.
解:(1)由 x+ x+ =0,得x=﹣4. =0,得x=﹣4.∴A点坐标为(﹣4,0), 由﹣2x+16=0,得x=8. ∴B点坐标为(8,0), ∴AB=8﹣(﹣4)=12, 由  ,解得 ,解得 , ,∴C点的坐标为(5,6), ∴S△ABC=  AB·CM= AB·CM= ×12×6=36; ×12×6=36;(2)∵点D在l1上,且xD=xB=8, ∴yD=  ×8+ ×8+ =8, =8,∴D点坐标为(8,8), 又∵点E在l2上,且yE=yD=8, ∴﹣2xE+16=8, ∴xE=4, ∴E点坐标为(4,8), ∴DE=8﹣4=4,EF=8; (3)①当0≤t<3时,如图1,矩形DEFG与△ABC重叠部分为五边形CHFGR(t=0时,为四边形CHFG). 过C作CM⊥AB于M,则Rt△RGB∽Rt△CMB, ∴  ,即 ,即 , ,∴RG=2t, ∵Rt△AFH∽Rt△AMC, ∴S=S△ABC﹣S△BRG﹣S△AFH=36﹣  ×t×2t﹣ ×t×2t﹣ (8﹣t)× (8﹣t)× (8﹣t), (8﹣t),即S=﹣  t2+ t2+ t+ t+ ; ;②当3≤t<8时,如图2所示,矩形DEFG与△ABC重叠部分为梯形HFGR,由①知,HF=  (8﹣t), (8﹣t),∵Rt△AGR∽Rt△AMC, ∴  = = ,即 ,即 = = , ,∴RG=  (12﹣t), (12﹣t),∴S=  (HF+RG)×FG= (HF+RG)×FG= [ [ (8﹣t)+ (8﹣t)+ (12﹣t)]×4,即S=﹣ (12﹣t)]×4,即S=﹣ t+ t+ ; ;③当8≤t≤12,如图3所示,矩形DEFG与△ABC重叠部分为△AGR, 由②知,AG=12﹣t,RG=  (12﹣t), (12﹣t),∴S=  AG·RG= AG·RG= (12﹣t)× (12﹣t)× (12﹣t),即S= (12﹣t),即S= (12﹣t)2, (12﹣t)2,∴S=  t2﹣8t+48. t2﹣8t+48. |
 图1  图2
 图3 |


科目:初中数学 来源: 题型:
 (2012•郯城县一模)如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )
(2012•郯城县一模)如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图:已知直线l1∥l2,且l3、l4和l1、l2分别交于点A、B和点C、D,点P在AB上,设∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.
如图:已知直线l1∥l2,且l3、l4和l1、l2分别交于点A、B和点C、D,点P在AB上,设∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.查看答案和解析>>
科目:初中数学 来源: 题型:
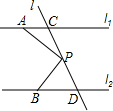 如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com