

分析 (1)过点B作BH⊥l交l于点H,解Rt△BCH,得出CH=BC•sin∠CBH=$\frac{27}{4}$,BH=BC•cos∠CBH=$\frac{27}{16}$.再解Rt△BAH中,求出AH=BH•tan∠ABH=$\frac{9}{4}$,那么根据AC=CH-AH计算即可;
(2)设他平时的速度为xkm/h,等量关系为:平时上班骑自行车所用的时间=提高了4.5km/h的速度后上班所用的时间+$\frac{20+10}{60}$小时,依此列出方程,进而求解即可.
解答 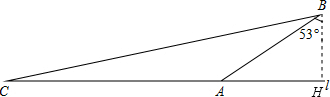 解:(1)过点B作BH⊥l交l于点H,
解:(1)过点B作BH⊥l交l于点H,
∵在Rt△BCH中,∠BHC=90°,∠CBH=76°,BC=7$\frac{1}{32}$km,
∴CH=BC•sin∠CBH≈$\frac{225}{32}$×$\frac{24}{25}$=$\frac{27}{4}$,BH=BC•cos∠CBH≈$\frac{225}{32}$×$\frac{6}{25}$=$\frac{27}{16}$.
∵在Rt△BAH中,∠BHA=90°,∠ABH=53°,BH=$\frac{27}{16}$,
∴AH=BH•tan∠ABH≈$\frac{27}{16}$×$\frac{4}{3}$=$\frac{9}{4}$,
∴AC=CH-AH=$\frac{27}{4}$-$\frac{9}{4}$=$\frac{9}{2}$.
(2)设他平时的速度为xkm/h,由题意得
$\frac{\frac{9}{2}}{x}$=$\frac{\frac{9}{2}}{x+4.5}$+$\frac{20+10}{60}$,
整理得2x2+9x-81=0,
解得x1=$\frac{9}{2}$,x2=-9(不合题意舍去),
经检验,x=$\frac{9}{2}$是原方程的根,也符合题意,
8+$\frac{\frac{9}{2}}{\frac{9}{2}}$=8+1=9,
答:他平时9点钟到达检查站A.
点评 本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
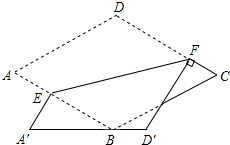 如图,菱形ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{FD}$的值为$\frac{\sqrt{3}-1}{2}$.
如图,菱形ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{FD}$的值为$\frac{\sqrt{3}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
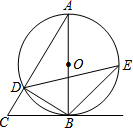 如图,已知△ABC,以AB为直径的⊙O交AC于点D,∠CBD=∠A.
如图,已知△ABC,以AB为直径的⊙O交AC于点D,∠CBD=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
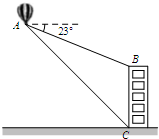 如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42.
如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
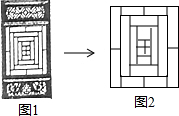 我国传统建筑中,窗框(如图1)的图案玲珑剔透、千变万化,窗框一部分如图2,它是一个轴对称图形,其对称轴有( )
我国传统建筑中,窗框(如图1)的图案玲珑剔透、千变万化,窗框一部分如图2,它是一个轴对称图形,其对称轴有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com