
 如图,平行于x轴的直线l与双曲线
如图,平行于x轴的直线l与双曲线 、
、 分别交于A、B两点,过A、B作x轴的垂线,垂足分别为C、D.若四边形ACDB的周长为8,且AB<AC,则点A的坐标是________.
分别交于A、B两点,过A、B作x轴的垂线,垂足分别为C、D.若四边形ACDB的周长为8,且AB<AC,则点A的坐标是________. ,3)
,3) ),利用AB平行于x轴,点B的纵坐标为
),利用AB平行于x轴,点B的纵坐标为 ,而点B在反比例函数y=-
,而点B在反比例函数y=- ,图象上,易得B点坐标为(-2a,
,图象上,易得B点坐标为(-2a, ),则AB=a-(-2a)=3a,AC=
),则AB=a-(-2a)=3a,AC= ,然后根据矩形的性质得到AB+AC=4,即3a+
,然后根据矩形的性质得到AB+AC=4,即3a+ =4,则3a2-4a+1=0,用因式分解法解得a1=
=4,则3a2-4a+1=0,用因式分解法解得a1= ,a2=1,而AB<AC,则a=
,a2=1,而AB<AC,则a= ,即可写出A点坐标.
,即可写出A点坐标. 图象上,设A点坐标为(a,
图象上,设A点坐标为(a, ),
), ,
, ,图象上,
,图象上, ),
), ,
, =4,
=4, ,a2=1,
,a2=1, ,
, ,3),
,3), ,3).
,3).

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
| 1 | 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 相交于点C.
相交于点C.
查看答案和解析>>
科目:初中数学 来源:2012届重庆万州区岩口复兴学校九年级下第一次月考数学试卷(带解析) 题型:解答题
已知:直角梯形AOBC在平面直角坐标系中的位置如图,若AC∥OB,OC平分∠AOB,CB⊥x轴于B,点A坐标为(3 ,4). 点P从原点O开始以2个单位/秒速度沿x轴正向运动 ;同时,一条平行于x轴的直线从AC开始以1个单位/秒速度竖直向下运动 ,交OA于点D,交OC于点M,交BC于点E. 当点P到达点B时,直线也随即停止运动. 
(1)求出点C的坐标;
(2)在这一运动过程中, 四边形OPEM是什么四边形?请说明理由。若
用y表示四边形OPEM的面积 ,直接写出y关于t的函数关系式及t的
范围;并求出当四边形OPEM的面积y的最大值?
(3)在整个运动过程中,是否存在某个t值,使⊿MPB为等腰三角形?
若有,请求出所有满足要求的t值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省扬州市邗江区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,抛物线 与x轴交于点A(—2,0),交y轴于点B(0,
与x轴交于点A(—2,0),交y轴于点B(0, ).直
).直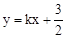 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.

(1)求抛物线 与直线
与直线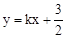 的解析式;
的解析式;
(2)设点P是直线AD下方的抛物线上一动点(不与点A、D重合),过点P作 y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为m,点P的横坐标为x,求m与x的函数关系式,并求出m的最大值.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年重庆万州区岩口复兴学校九年级下第一次月考数学试卷(解析版) 题型:解答题
已知:直角梯形AOBC在平面直角坐标系中的位置如图,若AC∥OB,OC平分∠AOB,CB⊥x轴于B,点A坐标为(3 ,4). 点P从原点O开始以2个单位/秒速度沿x轴正向运动 ;同时,一条平行于x轴的直线从AC开始以1个单位/秒速度竖直向下运动 ,交OA于点D,交OC于点M,交BC于点E. 当点P到达点B时,直线也随即停止运动.

(1)求出点C的坐标;
(2)在这一运动过程中, 四边形OPEM是什么四边形?请说明理由。若
用y表示四边形OPEM的面积 ,直接写出y关于t的函数关系式及t的
范围;并求出当四边形OPEM的面积y的最大值?
(3)在整个运动过程中,是否存在某个t值,使⊿MPB为等腰三角形?
若有,请求出所有满足要求的t值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com