
 ,p)时,①填空:p=_____,m=______,∠AOE=_______;
,p)时,①填空:p=_____,m=______,∠AOE=_______;
解:(1)①P=1,m= ,∠AOE=60°; ,∠AOE=60°;②连结TM、ME、EN,NQ、MQ(如图1) ∵OE切于点E,l∥x轴 ∴∠OEQ=∠QFM=90°,且NF=MF 又∵QF=2-1=1=EF, ∴四边形MENQ是平行四边形, ∴QN∥ME 在Rt△QFN中,QF=1,QN=2, ∴∠FQN=60° 依题意,在四边形OEQT中,∠TOE=60°,∠OTQ=∠OEQ=90°, ∴∠TQE=120° ∴∠TQE+∠NQE =180°, ∴T、Q、N在同一直线上 ∴ME∥TN,ME≠TN,且∠TMN=90°, 又∠TNM=30°, ∴MT=2, 又QE=QN=2, ∴△EQN为等边三角形, ∴EN=2, ∴EN=MT, ∴四边形MENT是等腰梯形; 注:也可证明∠MTN=∠ENT=60° |
|
| (2)a的值不变,理由如下: 如图,DE与MN交于点F,连结MD、ME, ∵DE是⊙O的直径, ∴∠DME=90°, 又∵∠MFD=90°, ∴∠MDE=∠EMN, ∴tan∠MDE=tan∠EMN , ∴  , ,即  (1) (注:本式也可由△MDF~△EMF得到) (1) (注:本式也可由△MDF~△EMF得到) ∵在平移过程中,图形的形状及特征保持不变,抛物线  的图象可通过 的图象可通过 的图象平移得到, 的图象平移得到,∴可以将问题转化为:点D在y轴上,点M、N在x轴上进行探索(如图2), 由图形的对称性可得点D为抛物线顶点, 依题意,得,设D(0,k)(k=2r-1>0),M(x1,0),N(x2,0)(x2<x2), 则经过M、D、N三点的抛物线为  , ,当y=0时,x1、x2为  的两根,解得 的两根,解得 , ,∴  , ,代入(1)式得  , ,∴  , ,又k>0, ∴a=-1, 故a的值不变。 |
|


科目:初中数学 来源: 题型:
| ||
| 3 |
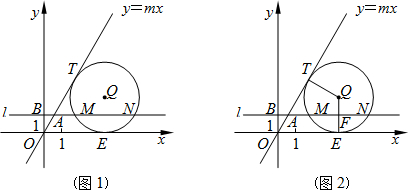
查看答案和解析>>
科目:初中数学 来源: 题型:
P点为抛物线![]() (
(![]() 为常数,
为常数,![]() )上任一点,将抛物线绕顶点
)上任一点,将抛物线绕顶点![]() 逆时针旋转
逆时针旋转![]() 后得到的新图象与
后得到的新图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的上方),点
的上方),点![]() 为点
为点![]() 旋转后的对应点.
旋转后的对应点.

1.(1)当![]() ,点
,点![]() 横坐标为4时,求
横坐标为4时,求![]() 点的坐标;
点的坐标;
2.(2)设点![]() ,用含
,用含![]() 、
、![]() 的代数式表示
的代数式表示![]() ;
;
3.(3) 如图,点![]() 在第一象限内, 点
在第一象限内, 点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 为
为![]() 的中点,
的中点,![]() 平分
平分![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2013年广东省深圳市中考数学模拟试卷(五)(解析版) 题型:解答题
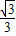 ,p)时,
,p)时,查看答案和解析>>
科目:初中数学 来源:2012年福建省泉州市中考数学试卷(样卷)(解析版) 题型:解答题
 ,p)时,
,p)时,查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建省泉州市九年级升学考试(样卷)数学试卷(解析版) 题型:解答题
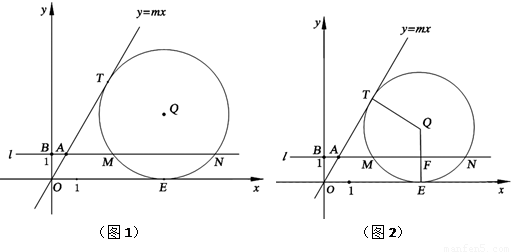
如图1,在第一象限内,直线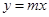 与过点
与过点 且平行于
且平行于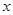 轴的直线
轴的直线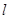 相交于点
相交于点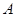 ,半径为
,半径为 的⊙
的⊙ 与直线
与直线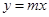 、
、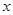 轴分别相切于点
轴分别相切于点 、
、 ,且与直线
,且与直线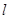 分别交于不同的
分别交于不同的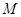 、
、 两点.
两点.
(1)当点A的坐标为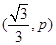 时,
时,
① 填空: = ,
= , = ,
= ,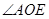 = ;
= ;
②如图2,连结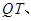
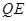 ,
,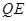 交直线
交直线 于
于 ,当
,当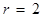 时,试说明以
时,试说明以 、
、
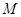 、
、 、
、 为顶点的四边形是等腰梯形;
为顶点的四边形是等腰梯形;
(2)在图1中,连结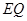 并延长交⊙
并延长交⊙ 于点
于点 ,试探索:对不同的
,试探索:对不同的 取值,经过
取值,经过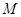 、
、 、
、 三点的抛物线
三点的抛物线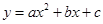 ,
,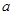 的值会变化吗?若不变,求出
的值会变化吗?若不变,求出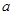 的值;若变化,请说明理由.
的值;若变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com