D
分析:求出∠ADC=∠BEC=90°,根据四边形内角和定理求出∠DOE,即可求出∠3,求出∠CAB+∠ABC,求出

(∠CAB+ABC),根据三角形内角和定理即可求出∠4;求出∠CAD=∠CBE=40°,求出∠1=

∠CAB-40°,∠2=

∠ABC-40°,即可判断③;根据三角形面积公式即可判断④.
解答:∵AD⊥BC,BE⊥AC,
∴∠BEC=∠ADC=90°,
∵∠C=50°,
∴∠DOE=360°-90°-90°-50°=130°,
∴∠3=180°-130°=50°,∴①正确;
∵∠C=50°,
∴∠ABC+∠BAC=180°-50°=130°,
∵AF、BG分别平分∠BAC、∠ABC,
∴∠FAB=

∠CAB,∠ABG=

∠ABC,
∴∠FAB+∠ABG=

(∠CAB+∠ABC)=

×130°=65°,
∴∠4=180°-(∠ABG+∠BAF)=180°-65°=115°,∴②正确;
∵AD⊥BC,BE⊥AC,
∴∠AEO=∠BDO=90°,
∵∠3=∠BOD=50°,
∴∠CBE=∠CAD=90°-50°=40°,
∵BG、AF分别平分∠CAB、∠ABC,
∴∠CAF=

∠CAB,∠CBG=

∠CBA,
∴∠2=

∠CBA-∠CBE=

∠CBA-40°,
同理∠1=

∠BAC-40°,
∵根据已知不能推出∠CAB=∠ABC,
∴不能推出∠1=∠2,∴③错误;
在△ABC中,由三角形面积公式得:

BC×AD=

AC×BE,
∴

=

,∴④正确;
故选D.
点评:本题考查三角形内角和定理的应用,主要考查学生运用定理进行推理和计算的能力,有一定的难度.

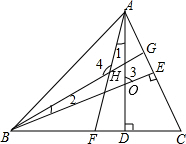
 如图,在△ABC中,AD、BE分别是BC、AC边上的高,AF、BG分别是△ABC中∠BAC,∠ABC的角平分线,∠C=50°,给出如下四个结论:
如图,在△ABC中,AD、BE分别是BC、AC边上的高,AF、BG分别是△ABC中∠BAC,∠ABC的角平分线,∠C=50°,给出如下四个结论: ,
, (∠CAB+ABC),根据三角形内角和定理即可求出∠4;求出∠CAD=∠CBE=40°,求出∠1=
(∠CAB+ABC),根据三角形内角和定理即可求出∠4;求出∠CAD=∠CBE=40°,求出∠1= ∠CAB-40°,∠2=
∠CAB-40°,∠2= ∠ABC-40°,即可判断③;根据三角形面积公式即可判断④.
∠ABC-40°,即可判断③;根据三角形面积公式即可判断④.
 ∠CAB,∠ABG=
∠CAB,∠ABG= ∠ABC,
∠ABC, (∠CAB+∠ABC)=
(∠CAB+∠ABC)= ×130°=65°,
×130°=65°, ∠CAB,∠CBG=
∠CAB,∠CBG= ∠CBA,
∠CBA, ∠CBA-∠CBE=
∠CBA-∠CBE= ∠CBA-40°,
∠CBA-40°, ∠BAC-40°,
∠BAC-40°, BC×AD=
BC×AD= AC×BE,
AC×BE, =
= ,∴④正确;
,∴④正确;

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为