
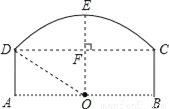
如图为桥洞的形状,其正视图是由弧CD和矩形ABCD构成.O点为弧CD所在⊙O的圆心,且点O恰好在水面AB上.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求弧CD所在⊙O的半径DO.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源:2016-2017学年内蒙古通辽市八年级(下)期末数学试卷 题型:填空题
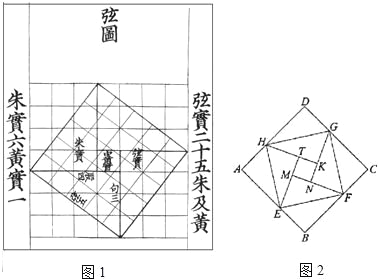
我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是_________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年内蒙古赤峰市七年级(上)期中数学试卷 题型:单选题
在下列数-3,+2.3,- 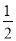 ,0.65,-2
,0.65,-2 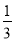 ,-2.5,0中,整数和负分数一共有
,-2.5,0中,整数和负分数一共有
A.3个 B.4个 C.5个 D.6个
C 【解析】整数有-3,0,负分数有-,-2,-2.5,一共5个,故选C。查看答案和解析>>
科目:初中数学 来源:内蒙古巴彦淖尔市2017-2018学年九年级(上)期中数学试卷 题型:单选题
如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
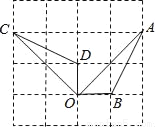
A. 30° B. 45° C. 90° D. 135°
C 【解析】试题分析:根据旋转的性质,对应边的夹角∠BOD即为旋转角. 【解析】 ∵△AOB绕点O按逆时针方向旋转到△COD的位置, ∴对应边OB、OD的夹角∠BOD即为旋转角, ∴旋转的角度为90°. 故选C.查看答案和解析>>
科目:初中数学 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:解答题
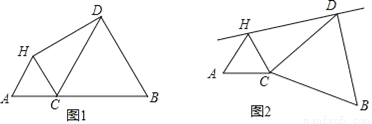
如图,C为线段AB上一点,分别以AC,BC为边在AB的同侧作等边△HAC与等边△DCB,连接DH.
(1)如图1,当∠DHC=90°时,求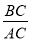 的值;
的值;
(2)在(1)的条件下,作点C关于直线DH的对称点E,连接AE,BE.求证:CE平分∠AEB.
(3)现将图1中的△DCB绕点C顺时针旋转一定角度α(0°<α<90°),如图2,点C关于直线DH的对称点为E,则(2)中的结论是否还成立,并证明.
查看答案和解析>>
科目:初中数学 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:填空题
已知关于x的方程x2﹣6x+k=0的两根分别 是x1,x2,且满足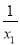 +
+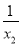 =3,则k的值是 _______.
=3,则k的值是 _______.
查看答案和解析>>
科目:初中数学 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:单选题
圆锥底面圆的半径为3cm,其侧面展开图是半圆,则圆锥母线长为( )
A.3cm B.6cm C.9cm D.12cm
B 【解析】 试题分析:首先根据圆的周长公式求得圆锥的底面周长=6π,然后根据圆锥的侧面展开图(扇形)的弧长等于底面周长,根据弧长公式即可求得母线长,可得母线长为6. 故选B.查看答案和解析>>
科目:初中数学 来源:贵州铜仁伟才学校2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
先化简,再求值: 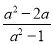 ÷(
÷(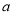 -1-
-1-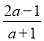 )其中
)其中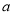 是方程
是方程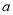 2+2
2+2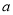 =8的一个根.
=8的一个根.
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市鄞州区2017-2018学年九年级上册数学第一次月考试卷 题型:单选题
一次函数y=ax+b和y=ax2+bx+c(a≠0)同一直角坐标系内的图象是( )
A. 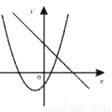 B.
B. 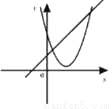 C.
C. 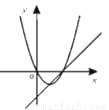 D.
D. 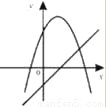
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com