练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    图（1）是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．如图（2）建立平面直角坐标系，则抛物线的关系式是（　　）

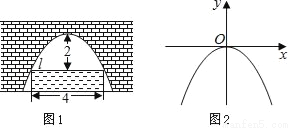
    A. y=﹣2x2 B. y=2x2 C. y=﹣0.5x2 D. y=0.5x2

    C 【解析】 由题意得，B（2，－2）， 设二次函数解析式为：y=ax2， 将B（2，－2）代入解析式得：－2=4a，解得a=－0.5. 所以函数解析式为y= －0.5x2. 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型：单选题

    直角三角形两直角边长为a，b，斜边上高为h，则下列各式总能成立的是（   ）

    A. ab=h2 B. a2+b2=2h2 C. 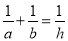D.

    D 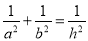【解析】根据直角三角形的面积可以导出：斜边c=． 再结合勾股定理：a2+b2=c2． 进行等量代换，得a2+b2=，两边同除以a2b2， 得． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：湖南省邵阳县黄亭市2017~2018学年九年级数学（上）期末综合检测模拟题 题型：填空题

    若关于x的一元二次方程x2 – 2x+k＝0无实数根，则实数k的取值范围是____．

    k＞1 【解析】试题解析：∵关于x的一元二次方程x2-2x+k=0无实数根， ∴△=b2-4ac=（-2）2-4×1×k＜0， ∴k＞1.

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：解答题

    如图，河的两岸l1与l2相互平行，A、B是l1上的两点，C、D是l2上的两点，某人在点A处测得∠CAB=90°，∠DAB=30°，再沿AB方向前进20米到达点E（点E在线段AB上），测得∠DEB=60°，求C、D两点间的距离．

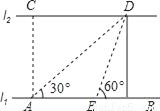
    C、D两点间的距离为30m． 【解析】直接利用等腰三角形的判定与性质得出DE=AE=20，进而求出EF的长，再得出四边形ACDF为矩形，则CD=AF=AE+EF求出答案． 【解析】 过点D作l1的垂线，垂足为F， ∵∠DEB=60°，∠DAB=30°， ∴∠ADE=∠DEB﹣∠DAB=30°， ∴△ADE为等腰三角形， ∴DE=AE=20， 在Rt△DE...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：填空题

    如图，在△ABC中，点D、E分别为边AC、AB上的点，且∠ADE=∠B，AE=3，BE=4，则AD•AC=　 　．

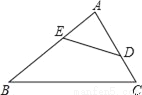
    21. 【解析】∵AE=3，BE=4，∴AB=AE+BE=7， ∵∠ADE=∠B，∠A=∠A，∴△ADE∽△ABC， ∴， 即， ∴AD·AC=21， 故答案为：21.

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：单选题

    连续四次抛掷一枚硬币都是正面朝上，则“第五次抛掷正面朝上”是（　　）

    A. 必然事件 B. 不可能事件

    C. 随机事件 D. 概率为1的事件

    C 【解析】硬币落地时，只有正面朝上和反面朝上两种情况，所以第五次抛掷正面朝上是随机事件， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：单选题

    如图所示的几何体是由5个大小相同的小正方体紧密摆放而成的，其三视图中面积最大的是（　　）

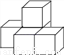
    A. 主视图 B. 左视图 C. 俯视图 D. 主视图和俯视图

    D 【解析】如图，该几何体主视图是由4个小正方形组成， 左视图是由3个小正方形组成， 俯视图是由4个小正方形组成，故三种视图面积最小的是左视图． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：山东省诸城市2018届九年级上学期期中联考数学试卷（Word版）. 题型：单选题

    如图是一个古代车轮的碎片，小明为求其外圆半径，连接外圆上的两点A，B，并使AB与车轮内圆相切于点D，半径OC⊥AB交外圆于点C，测得CD=10cm，AB=60cm，则这个车轮的外圆半径是（　　）

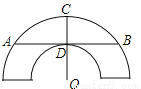
    A. 10cm B. 30cm C. 60cm D. 50cm

    D 【解析】试题分析：连接OB，根据垂径定理可得：BD=30cm，△BOD为直角三角形，设OB=rcm，则OD=(r-10)cm，根据Rt△BOD的勾股定理可得： ，解得：r=50cm，故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源九年一贯制学校中考数学模拟试卷 题型：填空题

    如图，已知△ABC中，AB=AC=1，∠BAC=120°，将△ABC绕点C顺时针旋转90°，得到△A′B′C，则点B运动的路径长为_____（结果保留π）

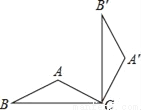
    【解析】过点A作AD⊥BC于D，首先由已知条件可求出BC的长，即点B旋转的半径，再根据弧长公式计算即可． 【解析】 过点A作AD⊥BC于D， ∵AB=AC=1，∠BAC=120°， ∴∠B=30°，∴BD=，∴BC=2BD=， ∵∠BCB′=90°， ∴点B运动的路径长=， 故答案为： ． “点睛”本题考查了旋转的性质、解直角三角形的运用以及弧长公式的运用，题目比较...

    查看答案和解析>>

    同步练习册答案