练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知点C是线段AB上的一点,不能确定点C是AB中点的条件是：

    A. AC=CB B. AC=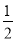AB C. AB=2BC D. AC+CB=AB

    D 【解析】选项A，若AC=BC，则C是线段AB中点；选项B，若AC=AB，则C是线段AB中点；选项C，若AB=2BC，则C是线段AB中点；选项D，AC+BC=AB，C可是线段AB是任意一点，则不能确定C是AB中点．故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市2018届2017年秋期期末冲刺卷 题型：单选题

    把函数y=﹣2x2的图象向左平移1个单位，再向上平移6个单位，所得的抛物线的函数关系式是（　　）

    A. y=﹣2（x﹣1）2+6 B. y=﹣2（x﹣1）2﹣6 C. y=﹣2（x+1）2+6 D. y=﹣2（x+1）2﹣6

    C 【解析】原抛物线的顶点坐标为(1,3),向左平移2个单位,再向上平移3个单位得到新抛物线的顶点坐标为(?1,6).可设新抛物线的解析式为：y=?2(x?h) ²+k,代入得：y=?2(x+1) ²+6. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市越秀区2016-2017学年八年级下册数学期末考试试卷 题型：单选题

    已知平面上四点A（0，0），B（10，0），C（12，6），D（2，6），直线y=mx﹣3m+6将四边形ABCD分成面积相等的两部分，则m的值为（   ）

    A. 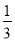B. ﹣1 C. 2 D.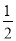

    B 【解析】如图，∵A（0，0），B（10，0），C（12，6），D（2，6）， ∴AB=10﹣0=10，CD=12﹣2=10， 又点C、D的纵坐标相同， ∴AB∥CD且AB=CD， ∴四边形ABCD是平行四边形， ∵12÷2=6，6÷2=3， ∴对角线交点P的坐标是（6，3）， ∵直线y=mx﹣3m+6将四边形ABCD分成面积相等的两部分， ...

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳市襄城区2016-2017学年度上学期期末考试七年级数学试卷 题型：解答题

    先化简,再求值:3x2y-[2x2y-3(2xy-x2y)-xy],其中x=-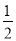,y=2.

    -8 【解析】试题分析：去小括号，去中括号，合并同类项，最后代入求出即可． 试题解析： 原式 当时， 原式

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳市襄城区2016-2017学年度上学期期末考试七年级数学试卷 题型：单选题

    甲队有51个人,乙队有45个人,从乙队调若干人到甲队后,甲队的人数恰好是乙队的3倍,求变化后乙队有多少人？若设变化后乙队有x人,可列方程为：

    A. 51+x=3(45-x) B. 51-x=3(45+x) C. 3x-51=45-x D. 51-3x=x-45

    C 【解析】试题解析：设变化后乙队有人，从乙队调若干人到甲队后,甲队的人数恰好是乙队的3倍，则调完后甲队有人，则从乙队调了人去甲队，甲队多得人数为： 方程为： 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（北师大版）：期中检测题 题型：解答题

    某公司为奖励在趣味运动会上取得好成绩的员工，计划购买甲、乙两种奖品共20件，其中甲种奖品每件40元，乙种奖品每件30元．

    （1）如果购买甲、乙两种奖品共花费了650元，求甲、乙两种奖品各购买了多少件；

    （2）如果购买乙种奖品的件数不超过甲种奖品件数的2倍，总花费不超过680元，求该公司有哪几种不同的购买方案．

    （1）购买的甲、乙两种奖品分别是5件、15件（2）该公司有两种不同的购买方案：方案一：购买甲种奖品7件，购买乙种奖品13件；方案二、购买甲种奖品8件，购买乙种奖品12件. 【解析】试题分析：（1）根据“两种奖品共20件”和“两种奖品共花费650元”列出方程组求解即可； （2）根据题意，列出不等式组求解即可. 试题解析：（1）设甲、乙两种奖品分别购买x件、y件 依题意，得： ...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（北师大版）：期中检测题 题型：填空题

    如图，把等边△A BC沿着D E折叠，使点A恰好落在BC边上的点P处，且DP⊥BC，若BP=4cm，则EC=______cm．

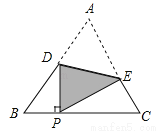
    【解析】∵△ABC是等边三角形，∴∠A=∠B=∠C=60°，AB=BC， ∵DP⊥BC，∴∠BPD=90°， ∵PB=4cm，∴BD=8cm，PD=cm， ∵把等边△A BC沿着D E折叠，使点A恰好落在BC边上的点P处， ∴AD=PD=cm，∠DPE=∠A=60°，∴AB=（8+）cm， ∴BC=（8+）cm，∴PC=BC﹣BP=（4+）cm， ∵∠EPC=1...

    查看答案和解析>>

    科目：初中数学 来源：重庆市校2017-2018学年八年级上学期第二阶段考试数学试卷 题型：解答题

    在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.

    （1）当直线MN绕点C旋转到图1的位置时，求证：DE=AD+BE；

    （2）当直线MN绕点C旋转到图2的位置时，求证：DE=AD-BE；

    （3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请直接写出这个等量关系.

    （1）证明见解析；（2）证明见解析；（3）DE=BE-AD. 【解析】试题分析：（1）由已知推出∠ADC=∠BEC=90°，因为∠ACD+∠BCE=90°，∠BCE+∠CBE=90°，推出∠ACD=∠CBE，根据AAS可得Rt△ADC≌Rt△CEB，得到AD=CE，CD=BE，即可求出答案； （2）与（1）证法类似可证出∠ACD=∠CBE，能推出△ADC≌△CEB，得到AD=CE，CD...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期中检测题 题型：单选题

    如图，函数y＝－x与函数y＝－的图象相交于A，B两点，过A，B两点分别作y轴的垂线，垂足分别为点C，D，则四边形ACBD的面积为(　　)

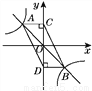
    A. 2 B. 4 C. 6 D. 8

    D 【解析】∵过函数y=?的图象上A，B两点分别作y轴的垂线，垂足分别为点C，D， ∴S△AOC=S△ODB=|k|=2， 又∵OC=OD，AC=BD， ∴S△AOC=S△ODA=S△ODB=S△OBC=2， ∴四边形ABCD的面积为：S△AOC+S△ODA+S△ODB+S△OBC=4×2=8. 故选：D.

    查看答案和解析>>

    同步练习册答案