
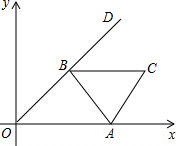
 边长为2的等边△ABC的顶点A在x轴的正半轴上移动,顶点B在射线OD上移动,∠AOD=45°,则顶点C到原点O的最大距离为________.
边长为2的等边△ABC的顶点A在x轴的正半轴上移动,顶点B在射线OD上移动,∠AOD=45°,则顶点C到原点O的最大距离为________. +
+
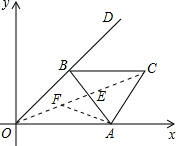 解:如图:
解:如图: =
= .AE=AC•cos60°=2×
.AE=AC•cos60°=2× =1.
=1. ,∠EAF=45°,
,∠EAF=45°, ,
, +1+
+1+ .
. +
+ .
.

科目:初中数学 来源: 题型:
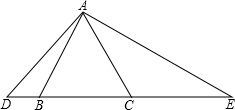 如图,△ABC是一个边长为2的等边三角形,D、E都在直线BC上,并且∠DAE=120°
如图,△ABC是一个边长为2的等边三角形,D、E都在直线BC上,并且∠DAE=120°查看答案和解析>>
科目:初中数学 来源: 题型:
 △ABC是边长为2的等边三角形,点P、Q分别从A、C两点同时出发做匀速直线运动,且它们的速度相等.已知点P沿边射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC,垂足是E.
△ABC是边长为2的等边三角形,点P、Q分别从A、C两点同时出发做匀速直线运动,且它们的速度相等.已知点P沿边射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC,垂足是E.查看答案和解析>>
科目:初中数学 来源:2013届河南长葛创新中学八年级上学期期末数学试卷(解析版) 题型:选择题
如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
A. B.
B. C.
C. D.不能确定
D.不能确定

查看答案和解析>>
科目:初中数学 来源:2010年全国中考试题分式专题训练 题型:选择题
如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )

A. B.
B. C.
C. D.不能确定
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com