解:由5AC-3AB=0,得到5AC=3AB,设AB为5xcm,则AC=3xcm,
在Rt△ABC中,由BC=8cm,根据勾股定理得:25x
2=9x
2+64,
解得:x=2,或x=-2(舍去),
∴AB=5x=10cm,AC=3x=6cm,
设经过t秒△ABC和△PQC相似.
则有BP=2tcm,PC=(8-2t)cm,CQ=tcm,
分两种情况:
①当△ABC∽△PQC时,有

,即
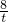
=

,解得

;
②当△ABC∽△QPC时,有

,即

,解得t=

,
综上可知,经过

或
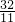
秒△ABC和△PQC相似.
分析:由AC与AB的关系,设出AC=3xcm与AB=5xcm,再由BC的长,在直角三角形ABC中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,进而得到AB与AC的长,然后设出动点运动的时间为ts,根据相应的速度分别表示出PC与CQ的长,由△ABC和△PQC相似,根据对应顶点不同分两种情况列出比例式,把各边的长代入即可得到关于t的方程,求出方程的解即可得到t的值,从而得到所有满足题意的时间t的值.
点评:此题考查了相似三角形的判定与性质,由已知的AC与AB的关系,利用勾股定理确定出两条边的长是本题的突破点,本题的关键是根据三角形相似的对应顶点不同,分两种情况△ABC∽△PQC与△ABC∽△QPC分别列出比例式来解决问题.

 如图,在△ABC中,∠C=90°,BC=8cm,5AC-3AB=0,点P从B出发,沿BC方向以2cm/s的速度移动,与此同时点Q从C出发,沿CA方向以1cm/s的速度移动,经过多长时间△ABC和△PQC相似?
如图,在△ABC中,∠C=90°,BC=8cm,5AC-3AB=0,点P从B出发,沿BC方向以2cm/s的速度移动,与此同时点Q从C出发,沿CA方向以1cm/s的速度移动,经过多长时间△ABC和△PQC相似? ,即
,即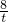 =
= ,解得
,解得 ;
; ,即
,即 ,解得t=
,解得t= ,
, 或
或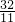 秒△ABC和△PQC相似.
秒△ABC和△PQC相似.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为