
已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(![]() ,0),⊙M的切线OC与直线AB交于点C.
,0),⊙M的切线OC与直线AB交于点C.

(1)求点B的坐标;
(2)求∠ACO的度数;
(3)求直线OC的函数解析式.
|
解:(1)∵∠AOB=90°, ∴线段AB为⊙M的直径, 1分 ∴AB=2. 2分 在Rt△ABO中,∵AO= 由勾股定理可解得OB=1, 3分 ∴点B的坐标为(0,1); 4分 (2)在Rt△ABO中,∵sin∠OAB= ∴∠OAB=30°. 5分 连结OM(如图),
∵MO=MA,∴∠MOA=∠MAO=30°, 6分 ∵OC切⊙M于点O,∴∠COM=90°, 7分 ∴∠COA=∠COM+∠MOA =90°+30°=120°, ∴∠ACO=180°-∠COA-∠CAO=30° 8分 (3)由(2)知∠OCA=∠OAC, ∴OC=OA= 过点C作CD⊥x轴于点D, ∠COD=180°-∠COA=60°, 9分 在Rt△OCD中, ∴OD=OC·cos∠COD = CD=OC·sin∠COD= ∵点C在第二象限,∴点C的坐标为(- 设直线OC的解析式为y=kx, 12分 把C点坐标代入其中,得k=- ∴直线OC的解析式为:y=- |


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
 于点A、B,点A的坐标为(
于点A、B,点A的坐标为(| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 23、已知:如图,⊙O半径为6.过⊙O外一点P作⊙O的切线PA,A为切点,∠OPA=30°.过PO与⊙O的交点B作直线BC交PA于点C,交⊙O于点D.
23、已知:如图,⊙O半径为6.过⊙O外一点P作⊙O的切线PA,A为切点,∠OPA=30°.过PO与⊙O的交点B作直线BC交PA于点C,交⊙O于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
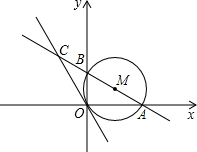 已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(
已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(| 3 |
查看答案和解析>>
科目:初中数学 来源:2008年广东省广州市白云区中考数学一模试卷(解析版) 题型:解答题
 ,0),⊙M的切线OC与直线AB交于点C.
,0),⊙M的切线OC与直线AB交于点C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com