
 当a≤x≤b时的最小值为2a,最大值为2b,求a、b的值.
当a≤x≤b时的最小值为2a,最大值为2b,求a、b的值. 解:函数
解:函数 的顶点是(0,
的顶点是(0, ),对称轴是y轴,最大值为
),对称轴是y轴,最大值为 ,如右图,
,如右图, a2+
a2+ =2a,
=2a, b2+
b2+ =2b,
=2b, x2+
x2+ =2x的两个根,
=2x的两个根, ,
, =2b,
=2b, ,
, ×(
×( )2+
)2+ =
= >0,而2a≤0,矛盾,
>0,而2a≤0,矛盾, )a2+
)a2+ =2a,
=2a, <0,符合条件,
<0,符合条件, )a2+
)a2+ =2b①,
=2b①, b2+
b2+ =2a②,
=2a②, )(a-b)(a+b)=2(b-a),
)(a-b)(a+b)=2(b-a), )a2+
)a2+ =2(4-a),
=2(4-a), ,b=
,b= .
.

 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
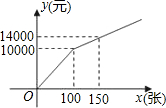 在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com