
如图①所示,已知△ABC中,a=5cm,b=3cm,c=4cm,∠B=![]() ,∠C=
,∠C=![]() ,请你从中选择适当的数据画一个三角形,使之与△ABC全等.把你所画的三角形全部画出,不写画法,但要保留作图痕迹.并在所画出的三角形中标出你选用到的数据,并说明符合条件的三角形可有多少种不同的画法?
,请你从中选择适当的数据画一个三角形,使之与△ABC全等.把你所画的三角形全部画出,不写画法,但要保留作图痕迹.并在所画出的三角形中标出你选用到的数据,并说明符合条件的三角形可有多少种不同的画法?

|
答案:从已知条件中任选三个可有六种不同的画法, (1)利用a=5cm,b=3cm,c=4cm可画出与△ABC全等的图形.如图②所示; (2)利用a=5cm,b=3cm,∠C= (3)利用a=5cm,c=4cm,∠B= (4)利用b=3cm,∠B= (5)利用c=4cm,∠B= (6)利用∠B= 剖析:依据全等三角形的判别方法可选择恰当的作图方案. |
|
方法提炼: 1.要画出与△ABC全等的三角形,可依据题设中所给出的五个数据中任选三个,利用SAS,SSS,ASA,AAS等分别尝试即可. 2.本题中的图⑤和图⑥利用AAS画△A4B4C4和△A5B5C5与已知△ABC全等时,同学们不太熟悉,为此不妨利用三角形内角和为 |


科目:初中数学 来源: 题型:
 (2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-
(2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-| 1 |
| 2 |
| 25 |
| 4 |
| 1 |
| 2 |
| (x2-x1)2+(y2-y1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 6 |
| x |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
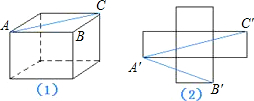 所示.已知展开图中每个正方形的边长为1.
所示.已知展开图中每个正方形的边长为1.查看答案和解析>>
科目:初中数学 来源: 题型:
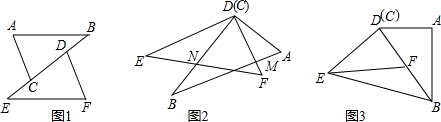
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com