
 =1-
=1- 用到等式性质2的是去分母和 ________.
用到等式性质2的是去分母和 ________.科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏泰州永安初级中学七年级12月练习数学试题(解析版) 题型:解答题
如图所示的两个长方形用不同形式拼成图1和图2两个图形.
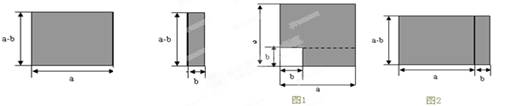
(1)若图1中的阴影部分面积为a2-b2;则图2中的阴影部分面积为______________.(用含字母a、b的代数式表示)
(2)由(1)你可以得到等式______________________________________;
(3)根据你所得到的等式解决下面的问题:
①计算:67.752-32.252
②解方程:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com