
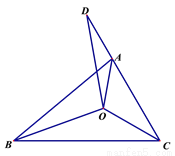
如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若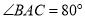 ,则
,则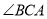 的度数为____________.
的度数为____________.
 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源:北京市东城区2017--2018学年第一学期期末练习初一数学试卷 题型:填空题
若∠1=35°21′,则∠1的余角是 。
54°39′. 【解析】 试题解析:根据定义,∠1的余角度数是90°-35°21′=54°39′.查看答案和解析>>
科目:初中数学 来源:湖北省武汉市武昌区2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
如图,点B、C在线段AD上,CD=2AB+3.
(1)若点C是线段AD的中点,求BC-AB的值;
(2)若BC=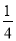 AD,求BC-AB的值;
AD,求BC-AB的值;
(3)若线段AC上有一点P(不与点B重合),AP+AC=DP,求BP的长.
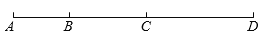
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市武昌区2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
若x=﹣1是关于x的方程2x+5a=3的解,则a的值为( )
A. 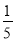 B. 4 C. 1 D. ﹣1
B. 4 C. 1 D. ﹣1
查看答案和解析>>
科目:初中数学 来源:安徽省芜湖市2017-2018学年度第一学期期末考试八年级数学试卷 题型:解答题
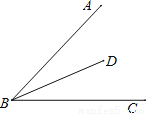
如图,点D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.
求证:BD平分∠ABC.
查看答案和解析>>
科目:初中数学 来源:安徽省芜湖市2017-2018学年度第一学期期末考试八年级数学试卷 题型:单选题
下列图形都是按照一定规律组成,第一图形中共有2个三角形,第二图形中共有8个三角形,第三个图形中共有14个三角形,……,依此规律,第六个图形中三角形的个数是( )

A. 32 B. 34 C. 36 D. 40
A 【解析】∵第一图形中共有2个三角形;2=2+6×0; 第二图形中共有8个三角形,8=2+6×1; 第三个图形中共有14个三角形,14=2+6×2; ……, ∴第六个图形中三角形的个数是:2+6×5=32(个).查看答案和解析>>
科目:初中数学 来源:安徽省芜湖市2017-2018学年度第一学期期末考试八年级数学试卷 题型:单选题
化简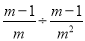 的结果是( )
的结果是( )
A. 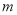 B.
B. 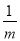 C.
C. 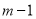 D.
D. 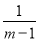
查看答案和解析>>
科目:初中数学 来源:安徽省亳州市涡阳县2017-2018学年度第一学期八年级期末联考数学试卷 题型:填空题
如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为 .
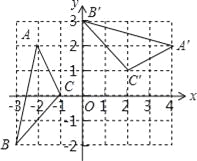
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市蓬溪县2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
已知:点P是直线MN外一点,点A、B、C是直线MN上三点,分别连接PA、PB、PC.
(1)通过测量的方法,比较PA、PB、PC的大小,直接用“>”连接;
(2)在直线MN上能否找到一点D,使PD的长度最短?如果有,请在图中作出线段PD,并说明它的理论依据;如果没有,请说明理由.
见解析 【解析】试题分析:(1)通过测量不难得出PA>PB>PC;由于点到直线的距离垂线段最短,所以过点P作PD⊥MN交MN于点D. 试题解析: 【解析】 (1)通过测量可知,PA>PB>PC; (2)过点P作PD⊥MN,则PD最短. (垂线段最短).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com