
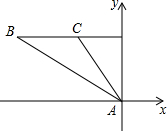
 某海关缉查艇在A处发现一艘可疑船只在其正北方向,以每小时20海里向正西方向逃窜,2小时后到达A的北偏西45°,此时缉查艇马上行动,沿北偏西60°方向进行拦截,一段时间后恰好在B处截获可疑船只,试求出缉查艇的速度.(精确到0.1海里)
某海关缉查艇在A处发现一艘可疑船只在其正北方向,以每小时20海里向正西方向逃窜,2小时后到达A的北偏西45°,此时缉查艇马上行动,沿北偏西60°方向进行拦截,一段时间后恰好在B处截获可疑船只,试求出缉查艇的速度.(精确到0.1海里) 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
 如图,A点、B点分别表示小岛码头、海岸码头的位置,离B点正东方向的7.00km处有一海岸瞭望塔C,又用经纬仪测出:A点分别在B点的北偏东57°处、在C点的东北方向.
如图,A点、B点分别表示小岛码头、海岸码头的位置,离B点正东方向的7.00km处有一海岸瞭望塔C,又用经纬仪测出:A点分别在B点的北偏东57°处、在C点的东北方向.查看答案和解析>>
科目:初中数学 来源: 题型:
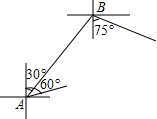 如图,在一次海上联合作战演习中,红方一艘侦察艇在A处发现在其北偏东30°方向,相距12海里的B处水面上,有蓝方一艘小艇正以每小时8海里的速度沿南偏东75°方向前进.若侦察艇以每小时16海里的速度,沿北偏东60°方向拦截蓝方的小艇.试问能否成功拦截?(
如图,在一次海上联合作战演习中,红方一艘侦察艇在A处发现在其北偏东30°方向,相距12海里的B处水面上,有蓝方一艘小艇正以每小时8海里的速度沿南偏东75°方向前进.若侦察艇以每小时16海里的速度,沿北偏东60°方向拦截蓝方的小艇.试问能否成功拦截?(| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
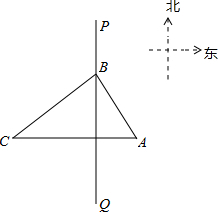 B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?
B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江杭州余杭九年级下学期阶段性测试数学试卷(解析版) 题型:解答题
如图,A点、B点分别表示小岛码头、海岸码头的位置,离B点正东方向的7.00km处有一海岸瞭望塔C,又用经纬仪测出:A点分别在B点的北偏东57°处、在C点的东北方向.

(1)试求出小岛码头A点到海岸线BC的距离;
(2)有一观光客轮K从B至A方向沿直线航行:
①某瞭望员在C处发现,客轮K刚好在正北方向的D处,试求出客轮驶出的距离BD的长;
②当客轮航行至E处时,发现E点在C的北偏东27°处,请求出E点到C点的距离;
(注:tan33°≈0.65,sin33°≈0.54,cos33°≈0.84,结果精确到0.01km)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com