
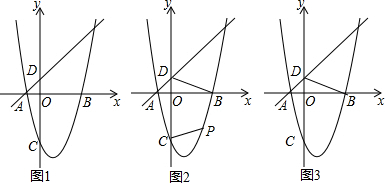
·ЦОц ЈЁ1Ј©ПИЗуөГөгAөДЧшұкЈ¬И»әуАыУГЕЧОпПЯөД¶ФіЖРФҝЙЗуөГөгBөДЧшұкЈ¬И»әуЗуөГөгCөДЧшұкЈ¬ЙиЕЧОпПЯөДҪвОцКҪОӘy=aЈЁx+1Ј©ЈЁx-3Ј©Ј¬Ҫ«CЈЁ0Ј¬-3Ј©ҙъИлЗуөГaөДЦөјҙҝЙЈ»
ЈЁ2Ј©Б¬ҪбOPЈ®ПИЗуөГөгDөДЧшұкЈ¬ҙУ¶шҝЙөГөҪODөДіӨЈ¬ЙиPЈЁtЈ¬t2-2t-3Ј©Ј¬И»әуТАҫЭЛДұЯРОDCPBөДГж»э=ЎчODBөДГж»э+ЎчOBPөДГж»э+ЎчOCPөДГж»эҝЙөГөҪSУлtөДәҜКэ№ШПөКҪЈ¬АыУГЕд·Ҫ·ЁҝЙЗуөГSөДЧоҙуЦөТФј°¶ФУҰөДtөДЦөЈ»
ЈЁ3Ј©ЙиөгDЎдөДЧшұкОӘЈЁaЈ¬a+1Ј©Ј¬OЎдЈЁaЈ¬aЈ©Ј¬өұЎчDЎдOЎдEөДГж»эЈәDЎдEBЎдөДГж»э=1Јә2КұЈ¬EЈЁa+1Ј¬aЈ©Ј¬Ҫ«өгEөДЧшұкҙъИлЕЧОпПЯөДҪвОцКҪҝЙЗуөГaөДЦөЈ¬ҙУ¶шөГөҪOЎдөДЧшұкЈ¬И»әуЗуөГOOЎдөДіӨјҙҝЙЈ¬өұЎчDЎдOЎдEөДГж»эЈәDЎдEBЎдөДГж»э=2Јә1КұЈ¬EЈЁa+2Ј¬aЈ©Ј¬Н¬АнҝЙЗуөГOOЎдөДіӨЈ¬ҙУ¶шҝЙөГөҪЎчBЎдOЎдDЎдЖҪТЖөДҫаАлЈ®
Ҫвҙр ҪвЈәЈЁ1Ј©°Сy=0ҙъИлЦұПЯөДҪвОцКҪөГЈәx+1=0Ј¬ҪвөГx=-1Ј¬
ЎаAЈЁ-1Ј¬0Ј©Ј®
ЎЯЕЧОпПЯөД¶ФіЖЦбОӘx=1Ј¬
ЎаBөДЧшұкОӘЈЁ3Ј¬0Ј©Ј®
Ҫ«x=0ҙъИлЕЧОпПЯөДҪвОцКҪөГЈәy=-3Ј¬
ЎаCЈЁ0Ј¬-3Ј©Ј®
ЙиЕЧОпПЯөДҪвОцКҪОӘy=aЈЁx+1Ј©ЈЁx-3Ј©Ј¬Ҫ«CЈЁ0Ј¬-3Ј©ҙъИлөГЈә-3a=-3Ј¬ҪвөГa=1Ј¬
ЎаЕЧОпПЯөДҪвОцКҪОӘy=x2-2x-3Ј®
ЈЁ2Ј©ИзНј1ЛщКҫЈәБ¬ҪбOPЈ®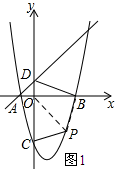
Ҫ«x=0ҙъИлЦұПЯADөДҪвОцКҪөГЈәy=1Ј¬
ЎаOD=1Ј®
УЙМвТвҝЙЦӘPЈЁtЈ¬t2-2t-3Ј©Ј®
ЎЯЛДұЯРОDCPBөДГж»э=ЎчODBөДГж»э+ЎчOBPөДГж»э+ЎчOCPөДГж»эЈ¬
ЎаS=$\frac{1}{2}$ЎБ3ЎБ1+$\frac{1}{2}$ЎБ3ЎБЈЁ-t2+2t+3Ј©+$\frac{1}{2}$ЎБ3ЎБtЈ¬ХыАнөГЈәS=-$\frac{3}{2}$t2+$\frac{9}{2}$t+6Ј®
Ед·ҪөГЈәS=-$\frac{3}{2}$ЈЁt-$\frac{3}{2}$Ј©2+$\frac{75}{8}$Ј®
Ўаөұt=$\frac{3}{2}$КұЈ¬SИЎөГЧоҙуЦөЈ¬ЧоҙуЦөОӘ$\frac{75}{8}$Ј®
ЈЁ3Ј©ИзНј2ЛщКҫЈә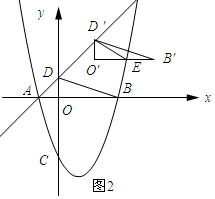
ЙиөгDЎдөДЧшұкОӘЈЁaЈ¬a+1Ј©Ј¬OЎдЈЁaЈ¬aЈ©Ј®
өұЎчDЎдOЎдEөДГж»эЈәDЎдEBЎдөДГж»э=1Јә2КұЈ¬ФтOЎдEЈәEBЎд=1Јә2Ј®
ЎЯOЎдBЎд=0B=3Ј¬
ЎаOЎдE=1Ј®
ЎаEЈЁa+1Ј¬aЈ©Ј®
Ҫ«өгEөДЧшұкҙъИлЕЧОпПЯөДҪвОцКҪөГЈәЈЁa+1Ј©2-2ЈЁa+1Ј©-3=aЈ¬ХыАнөГЈәa2-a-4=0Ј¬ҪвөГЈәa=$\frac{1+\sqrt{17}}{2}$»тa=$\frac{1-\sqrt{17}}{2}$Ј®
ЎаOЎдөДЧшұкОӘЈЁ$\frac{1+\sqrt{17}}{2}$Ј¬$\frac{1+\sqrt{17}}{2}$Ј©»тЈЁ$\frac{1-\sqrt{17}}{2}$Ј¬$\frac{1-\sqrt{17}}{2}$Ј©Ј®
ЎаOOЎд=$\frac{\sqrt{2}+\sqrt{34}}{2}$»тOOЎд=$\frac{\sqrt{34}-\sqrt{2}}{2}$Ј®
ЎаЎчDOBЖҪТЖөДҫаАлОӘ$\frac{\sqrt{2}+\sqrt{34}}{2}$»т$\frac{\sqrt{34}-\sqrt{2}}{2}$Ј®
өұЎчDЎдOЎдEөДГж»эЈәDЎдEBЎдөДГж»э=2Јә1КұЈ¬ФтOЎдEЈәEBЎд=2Јә1Ј®
ЎЯOЎдBЎд=0B=3Ј¬
ЎаOЎдE=2Ј®
ЎаEЈЁa+2Ј¬aЈ©Ј®
Ҫ«өгEөДЧшұкҙъИлЕЧОпПЯөДҪвОцКҪөГЈәЈЁa+2Ј©2-2ЈЁa+2Ј©-3=aЈ¬ХыАнөГЈәa2-a-4=0Ј¬ҪвөГЈәa=$\frac{-1+\sqrt{13}}{2}$»тa=$\frac{-1-\sqrt{13}}{2}$Ј®
ЎаOЎдөДЧшұкОӘЈЁ$\frac{-1+\sqrt{13}}{2}$Ј¬$\frac{-1+\sqrt{13}}{2}$Ј©»тЈЁ$\frac{-1-\sqrt{13}}{2}$Ј¬$\frac{-1-\sqrt{13}}{2}$Ј©Ј®
ЎаOOЎд=$\frac{-\sqrt{2}+\sqrt{26}}{2}$»тOOЎд=$\frac{\sqrt{2}+\sqrt{26}}{2}$Ј®
ЎаЎчDOBЖҪТЖөДҫаАлОӘ$\frac{-\sqrt{2}+\sqrt{26}}{2}$»т$\frac{\sqrt{2}+\sqrt{26}}{2}$Ј®
ЧЫЙПЛщКцЈ¬өұЎчDЎдOЎдBЎдСШDA·ҪПтЖҪТЖ$\frac{\sqrt{2}+\sqrt{34}}{2}$»т$\frac{\sqrt{2}+\sqrt{26}}{2}$өҘО»іӨ¶ИЈ¬»тСШAD·ҪПтЖҪТЖ$\frac{\sqrt{34}-\sqrt{2}}{2}$»т$\frac{-\sqrt{2}+\sqrt{26}}{2}$ёцөҘО»іӨ¶ИКұЈ¬EDЎдЗЎәГҪ«ЎчOЎдDЎдBЎдөДГж»э·ЦОӘ1Јә2БҪІҝ·ЦЈ®
өгЖА ұҫМвЦчТӘҝјІйөДКЗ¶юҙОәҜКэәҜКэөДЧЫәПУҰУГЈ¬ҪвҙрұҫМвЦчТӘУҰУГБЛҙэ¶ЁПөКэ·ЁЗу¶юҙОәҜКэөДҪвОцКҪЎў¶юҙОәҜКэөДРФЦКЎўЖҪТЖУлЧшұкұд»»Ј¬ТАҫЭЛДұЯРОDCPBөДГж»э=ЎчODBөДГж»э+ЎчOBPөДГж»э+ЎчOCPөДГж»эБРіцSУлtөДәҜКэ№ШПөКҪКЗҪвҙрОКМвЈЁ2Ј©өД№ШјьЈ¬УГә¬aөДКҪЧУұнКҫіцөгEөДЧшұкКЗҪвҙрОКМвЈЁ3Ј©өД№ШјьЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
 ёЯМъёшОТГЗөДіцРРҙшАҙБЛј«ҙуөД·ҪұгЈ®ИзНјЈ¬Ў°әНРіәЕЎұёЯМъБРіөЧщТОәуГжөДРЎЧА°еКХЖрКұЈ¬РЎЧА°еөДЦ§јЬөДөЧ¶ЛNУлЧАГж¶Ҙ¶ЛMөДҫаАлMN=75cmЈ¬ЗТҝЙТФҝҙЧчУлөШГжҙ№ЦұЈ®Х№ҝӘРЎЧА°еК№ЧАГжұЈіЦЛ®ЖҪЈ¬ABЎНMNЈ¬ЎПMAB=ЎПMNB=37ЎгЈ¬ЗТЦ§јЬіӨBNУлЧАГжҝнABөДіӨ¶ИЦ®әНөИУЪMNөДіӨ¶ИЈ®ЗуРЎЧА°еЧАГжөДҝн¶ИABЈЁҪб№ыҫ«И·өҪ1cmЈ¬ІОҝјКэҫЭЈәsin37ЎгЎЦ0.6Ј¬cos37ЎгЎЦ0.8Ј¬tan37ЎгЎЦ0.75Ј©
ёЯМъёшОТГЗөДіцРРҙшАҙБЛј«ҙуөД·ҪұгЈ®ИзНјЈ¬Ў°әНРіәЕЎұёЯМъБРіөЧщТОәуГжөДРЎЧА°еКХЖрКұЈ¬РЎЧА°еөДЦ§јЬөДөЧ¶ЛNУлЧАГж¶Ҙ¶ЛMөДҫаАлMN=75cmЈ¬ЗТҝЙТФҝҙЧчУлөШГжҙ№ЦұЈ®Х№ҝӘРЎЧА°еК№ЧАГжұЈіЦЛ®ЖҪЈ¬ABЎНMNЈ¬ЎПMAB=ЎПMNB=37ЎгЈ¬ЗТЦ§јЬіӨBNУлЧАГжҝнABөДіӨ¶ИЦ®әНөИУЪMNөДіӨ¶ИЈ®ЗуРЎЧА°еЧАГжөДҝн¶ИABЈЁҪб№ыҫ«И·өҪ1cmЈ¬ІОҝјКэҫЭЈәsin37ЎгЎЦ0.6Ј¬cos37ЎгЎЦ0.8Ј¬tan37ЎгЎЦ0.75Ј©Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
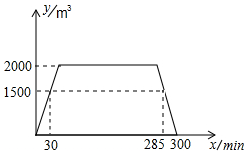 ДіУОУҫіШТ»МмТӘҫӯ№эЎ°ЧўЛ®-ұЈіЦ-ЕЕЛ®ЎұИэёц№эіМЈ¬ИзНјЈ¬НјЦРХЫПЯұнКҫөДКЗУОУҫіШФЪТ»МмДіТ»Кұјд¶ОДЪіШЦРЛ®БҝyЈЁm3Ј©УлКұјдxЈЁminЈ©Ц®јдөД№ШПөЈ®
ДіУОУҫіШТ»МмТӘҫӯ№эЎ°ЧўЛ®-ұЈіЦ-ЕЕЛ®ЎұИэёц№эіМЈ¬ИзНјЈ¬НјЦРХЫПЯұнКҫөДКЗУОУҫіШФЪТ»МмДіТ»Кұјд¶ОДЪіШЦРЛ®БҝyЈЁm3Ј©УлКұјдxЈЁminЈ©Ц®јдөД№ШПөЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәМоҝХМв
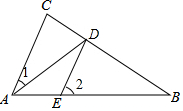 ИзНјЈ¬ТСЦӘADЖҪ·ЦЎПCABЈ¬DEЎОACЈ¬ЎП1=30ЎгЈ¬ФтЎП2=60ЎгЈ®
ИзНјЈ¬ТСЦӘADЖҪ·ЦЎПCABЈ¬DEЎОACЈ¬ЎП1=30ЎгЈ¬ФтЎП2=60ЎгЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | x1Јјx2Јјx3 | BЈ® | x1Јјx3Јјx2 | CЈ® | x2Јјx1Јјx3 | DЈ® | x3Јјx2Јјx1 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com