练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在⊙O中＝＝，则与∠ABC相等的角有________个．

    答案：3
    提示：

    (点拨：∠ACB＝∠DAC＝∠ADC．)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：101网校同步练习　初一数学　人教版(新课标2004年初审) 人教版(新课标2004年初审) 题型：044

    如图，在△ABC中，∠ABC与∠ACB的平分线交于点I，根据下列条件求∠BIC的度数．

    (1)若∠ABC＝50°，∠ACB＝80°，则∠BIC＝________；

    (2)若∠ABC＋∠ACB＝116°，则∠BIC＝________；

    (3)若∠A＝56°，则∠BIC＝________；

    (4)若∠BIC＝100°，则∠A＝________；

    (5)通过以上计算，探索出您所发现规律：∠A与∠BIC之间的数量关系是________．

    证明：

    查看答案和解析>>

    科目：初中数学 来源：三点一测丛书九年级数学上 题型：059

    正弦定理

    　　命题：如图，在锐角△ABC中，BC＝a．CA＝b．AB＝c，△ABC的外接圆半径为R．则＝2R．

    　　证明：连接CO并延长交O于点D．连接DB．则∠D＝∠A．

    　　∵CD为O的直径，∴∠DBC＝．在Rt△DBC中

    　　∵sinD＝．∴sinA＝，即＝2R．

    　　同理＝2R．＝2R．

    　　∴＝2R．

    请你阅读前面所给的命题及其证明后，完成下面的(1)、(2)两小题：

    (1)前面的阅读材料中略去了＝2R和＝2R”的证明过程，请你把＝2R”的证明过程补写出来．

    (2)直接用前面阅读材料中命题的结论解题．

    已知：如图，在锐角△ABC中，BC＝，CA＝，∠A＝．求△ABC的外接圆半径R及∠C．

    　

    查看答案和解析>>

    科目：初中数学 来源：2013年辽宁省辽阳市高级中等学校招生考试数学 题型：044

    定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”

    性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等，

    理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD＝S△BCD．

    应用：如图②，在矩形ABCD中，AB＝4，BC＝6，点E在AD上，点F在BC上，AE＝BF，AF与BE交于点O，

    (1)求证：△AOB和△AOE是“友好三角形”；

    (2)连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积，

    探究：在△ABC中，∠A＝30°，AB＝4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得到△CD与△ABC重合部分的面积等于△ABC面积的，请直接写出△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（12，0）、（12，6），直线y＝－x＋b与y轴交于点P，与边OA交于点D，与边BC交于点E．
    【小题1】若直线y＝－x＋b平分矩形OABC的面积，求b的值；
    【小题2】在（1）的条件下，当直线y＝－x＋b绕点P顺时针旋转时，与直线BC和x轴分别交于点N、M，问：是否存在ON平分∠CNM的情况？若存在，求线段DM的长；若不存在，请说明理由；
    【小题3】在（1）的条件下，将矩形OABC沿DE折叠，若点O落在边BC上，求出该点坐标；若不在边BC上，求将（1）中的直线沿y轴怎样平移，使矩形OABC沿平移后的直线折叠，点O恰好落在边BC上

    查看答案和解析>>

    科目：初中数学 来源： 题型：

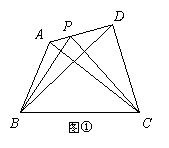
    提出问题：如图①，在四边形ABCD中，P是AD边上任意一点，△PBC与△ABC和△DBC的面积之间有什么关系？

    探究发现：为了解决这个问题，我们可以先从一些简单的、特殊的情形入手：

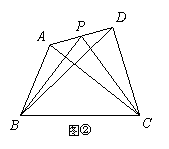
    （1）当AP＝AD时（如图②）：

    ∵AP＝AD，△ABP和△ABD的高相等，

    ∴S△ABP＝S△ABD ．

    ∵PD＝AD－AP＝AD，△CDP和△CDA的高相等，

    ∴S△CDP＝S△CDA ．

    ∴S△PBC ＝S四边形ABCD－S△ABP－S△CDP

    ＝S四边形ABCD－S△ABD－S△CDA

    ＝S四边形ABCD－(S四边形ABCD－S△DBC)－(S四边形ABCD－S△ABC)

    ＝S△DBC＋S△ABC ．

    （2）当AP＝AD时，探求S△PBC与S△ABC和S△DBC之间的关系，写出求解过程；

    （3）当AP＝AD时，S△PBC与S△ABC和S△DBC之间的关系式为：________________；

    （4）一般地，当AP＝AD（n表示正整数）时，探求S△PBC与S△ABC和S△DBC之间的关系，写出求解过程；

    问题解决：当AP＝AD（0≤≤1）时，S△PBC与S△ABC和S△DBC之间的关系式为：___________．

    查看答案和解析>>

    同步练习册答案