练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    甲、乙、丙三位选手各10次射击成绩的平均数和方差,统计如下表:

    选手

    甲

    乙

    丙

    平均数

    9.3

    9.3

    9.3

    方差

    0.026

    0.015

    0.032

    则射击成绩最稳定的选手是________.(填“甲”“乙”“丙”中的一个)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：云南省楚雄州2017-2018学年七年级下学期期末教学质量监测数学试卷 题型：填空题

    －的倒数是____．

    查看答案和解析>>

    科目：初中数学 来源：贵州省铜仁市2018年中考数学试卷 题型：填空题

    已知在平面直角坐标系中有两点A（0，1），B（﹣1，0），动点P在反比例函数y=的图象上运动，当线段PA与线段PB之差的绝对值最大时，点P的坐标为_____．

    查看答案和解析>>

    科目：初中数学 来源：贵州省铜仁市2018年中考数学试卷 题型：单选题

    9的平方根是

    A. 3 B. –3 C. 3和–3 D. 81

    查看答案和解析>>

    科目：初中数学 来源：安徽省毕业考试模拟冲刺数学卷(四) 题型：解答题

    探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:

    当n=2时,钉子板上所连不同线段的长度值只有1与，所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;

    当n=3时,钉子板上所连不同线段的长度值只有1, ，2, ，2五种,比n=2时增加了3种,即S=2+3=5.

    (1)观察图形,填写下表:

    钉子数(n×n)

    S值

    2×2

    2

    3×3

    2+3

    4×4

    2+3+（____）

    5×5

    （________）

    (2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).

    (3)对n×n的钉子板,写出用n表示S的代数式.

    查看答案和解析>>

    科目：初中数学 来源：安徽省毕业考试模拟冲刺数学卷(四) 题型：单选题

    （2013年四川自贡4分）如图，点O是正六边形的对称中心，如果用一副三角板的角，借助点O（使该角的顶点落在点O处），把这个正六边形的面积n等分，那么n的所有可能取值的个数是（ ）

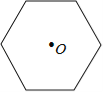
    A. 4 B. 5 C. 6 D. 7

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级中考数学模拟试卷 题型：解答题

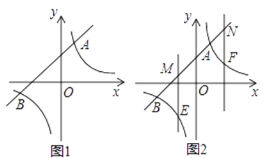
    如图1所示,一次函数y=kx+b的图象与反比例函数y= 的图象交A(1,4)，B(-4,c)两点,

    如图2所示,点M、N都在直线AB上,过M、N分别作y轴的平行线交双曲线于E、F,设M、N的横坐标分别为m、n,且 ? 4 < m < 0 , n > 1  ,请探究,当m、n满足什么关系时，ME=NE.

    （1）求反比例函数及一次函数的解析式;

    （2）点P是x轴上一动点,使|PA-PB|的值最大,求点P的坐标及△PAB的面积;

    （3）如图2所示,点M、N都在直线AB上,过M、N分别作y轴的平行线交双曲线于E、F,设M、N的横坐标分别为m、n,且 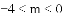, n>1 ,请探究,当m、n满足什么关系时，ME=NE.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级中考数学模拟试卷 题型：单选题

    下列无理数中，与最接近的是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源：江西省九江市2017-2018学年度七年级下学期期末考试数学试卷 题型：解答题

    动点型问题是数学学习中的常见问题，解决这类问题的关键是动中求静，运用分类讨论及数形结合的思想灵活运用有关数学知识解决问题。如图，在直角三角形ABC中，∠ACB=900，BC=4cm，AC=10cm，点D在射线CA上从点C出发向点A方向运动（点D不与点A重合），且点D运动的速度为2cm/s，设运动时间为x秒时，对应的△ABD的面积为ycm2.

    （1）填写下表：

    时间x秒

    ···

    2

    4

    6

    ···

    面积ycm2

    ···

    12

    ···

    （2）在点D的运动过程中，出现△ABD为等腰三角形的次数有________ 次，请用尺规作图，画出BD（保留作图痕迹，不写画法）；

    （3）求当x为何值时，△ABD的面积是△ABC的面积的.

    查看答案和解析>>

    同步练习册答案