
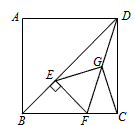
| 解:(1)在Rt△FCD中, ∵G为DF的中点, ∴CG= 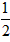 FD, FD,同理,在Rt△DEF中,EG= 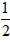 FD, FD,∴CG=EG; |
|
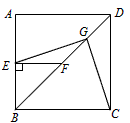
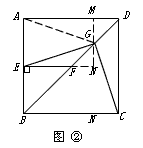
| (2)(1)中结论仍然成立,即EG=CG, 连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点, 在△DAG与△DCG中, ∵AD=CD,∠ADG=∠CDG,DG=DG, ∴△DAG≌△DCG, ∴AG=CG, 在△DMG与△FNG中, ∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG, ∴△DMG≌△FNG, ∴MG=NG, 在矩形AENM中,AM=EN, 在Rt△AMG 与Rt△ENG中, ∵AM=EN,MG=NG, ∴△AMG≌△ENG, ∴AG=EG, ∴EG=CG; |
 |
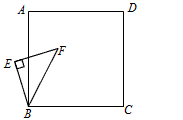
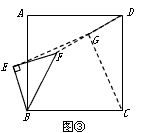
| (3)(1)中的结论仍然成立,即EG=CG, 其他的结论还有:EG⊥CG。 |
 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.
如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.查看答案和解析>>
科目:初中数学 来源: 题型:
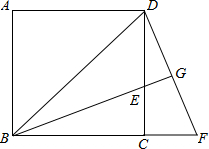 (2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.
如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com